
点(2,y1),(3,y2)在函数y=-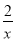 的图象上,则y1________y2(填“>”“<”或“=”).
的图象上,则y1________y2(填“>”“<”或“=”).
科目:初中数学 来源:江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型:单选题
某市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物)指数如下表,则该周PM2.5指数的众数和中位数分别是( )
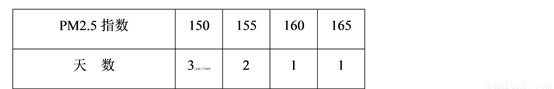
A. 150,150 B. 150,155 C. 155,150 D. 150,152.5
B 【解析】试题解析:这组数据按照从小到大的顺序排列为:150,150,150,155,155,160,165, 则众数为:150, 中位数为:155. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年北师大版七年级数学下1.2幂的乘方与积的乘方同步练习(含答案) 题型:单选题
计算(﹣3a2)2的结果是( )
A.3a4 B.﹣3a4 C.9a4 D.﹣9a4
C 【解析】 根据积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘计算即可. 【解析】 (﹣3a2)2=32a4=9a4. 故选C.查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:解答题
如图,正比例函数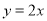 的图象与反比例函数
的图象与反比例函数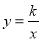 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
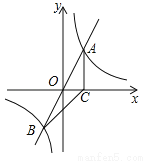
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
(1)k=2;(2)D(5,0)或(﹣5,0)或(,0)或D(,0). 【解析】试题分析:(1)首先根据反比例函数与正比例函数的图象特征,可知A、B两点关于原点对称,则O为线段AB的中点,故△BOC的面积等于△AOC的面积,都等于1,然后由反比例函数的比例系数k的几何意义,可知△AOC的面积等于,从而求出k的值; (2)先将与联立成方程组,求出A、B两点的坐标,然后分三种情况讨论:①当...查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:单选题
如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A.C分别在x轴、y轴上,反比例函数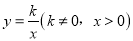 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=450,MN=2,则点C的坐标为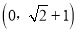 .
.
其中正确的个数是( )
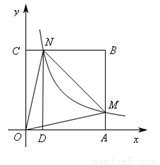
A.1 B.2 C.3 D.4
C. 【解析】 试题分析:设正方形OABC的边长为a, 则A(a,0),B(a,a),C(0,a),M(a,),N(,a). ∵CN=AM=,OC=OA= a,∠OCN=∠OAM=900,∴△OCN≌△OAM(SAS).结论①正确. 根据勾股定理,,,∴ON和MN不一定相等.结论②错误. ∵,∴.结论③正确. 如图,过点O作OH⊥MN于点H,则 ∵△...查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:单选题
函数y=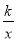 与y=kx+k(k为常数且k≠0)在同一平面直角坐标系中的图象可能是( )
与y=kx+k(k为常数且k≠0)在同一平面直角坐标系中的图象可能是( )
A. 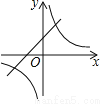 B.
B. 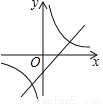 C.
C. 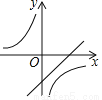 D.
D. 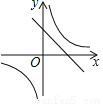
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:单选题
下面的函数是反比例函数的是( )
A. y=3x-1 B. y=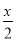 C. y=
C. y=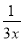 D. y=
D. y=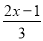
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第1章 有理数 单元测试卷 题型:单选题
如图,数轴上有A,B,C,D四个点,其中表示2的相反数的点是( )
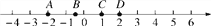
A. 点A B. 点B C. 点C D. 点D
A 【解析】试题解析:数轴上表示2的相反数的点是-2,即A点. 故选A.查看答案和解析>>
科目:初中数学 来源:四川省仁寿县2017-2018学年上学期八年级期末考试数学试卷 题型:填空题
如图,∠ABF=∠DCE,BE=CF,请补充一个条件:______,能使用“AAS”的方法得△ABF≌△DCE.
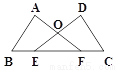
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com