
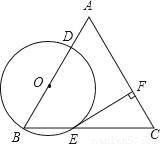
��֪����ABC�DZ߳�Ϊ4�ĵȱ������Σ���O�ڱ�AB�ϣ���O����B�ҷֱ����AB��BC�ཻ�ڵ�D��E��EF��AC������ΪF��
��1����֤��ֱ��EF�ǡ�O�����ߣ�
��2����ֱ��DF���O����ʱ�����O�İ뾶��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�������г�����2017-2018ѧ�����꼶���ϣ�������ѧ ���ͣ������
������ʽ x2yn�멁2xmy3�ĺ���Ϊ����ʽ����nm��ֵΪ_____��
x2yn�멁2xmy3�ĺ���Ϊ����ʽ����nm��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�������п���ѧģ���Ծ������� ���ͣ������
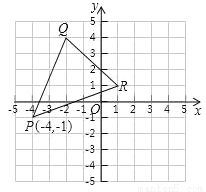
��֪����ͼ���ڰ뾶Ϊ4�ġ�O�У�AB��CD������ֱ����MΪOB���е㣬CM���ӳ��߽���O�ڵ�E����EM��MC������DE��DE=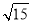 ��
��
��1����֤��AM•MB=EM•MC��
��2����EM�ij���
��3����sin��EOB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�������п���ѧģ���Ծ������� ���ͣ���ѡ��
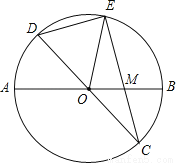
��ͼ������PQR����ƽ��2����λ���ȣ�������ƽ��3����λ���ȣ���Pƽ�ƺ�������ǣ� ��
A������2����4�� B������2��4�� C����2����3�� D������1����3��
A�� �������� ����������������֪��������ǣ�x+2��y��3�����մ˹��ɼ����֪����P����4����1��ƽ�ƺ�������ǣ���2����4������ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�������п���ѧģ���Ծ������� ���ͣ���ѡ��
�������ʽ��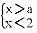 ǡ��3�������⣬��a��ȡֵ��Χ�ǣ�������
ǡ��3�������⣬��a��ȡֵ��Χ�ǣ�������
A. a�ܩ�1 B. a����1 C. ��2��a����1 D. ��2��a�ܩ�1
C ������������������߲���ʽǡ����3�������⣬ ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�������п���ѧģ���Ծ���ʮ�� ���ͣ������
��������������y= ��k��1����y=
��k��1����y= �ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y=
�ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y= ��ͼ���ϣ�PC��x���ڵ�C����y=
��ͼ���ϣ�PC��x���ڵ�C����y= ��ͼ���ڵ�A��PD��y���ڵ�D����y=
��ͼ���ڵ�A��PD��y���ڵ�D����y= ��ͼ���ڵ�B��BE��x���ڵ�E������P��y=
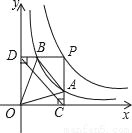
��ͼ���ڵ�B��BE��x���ڵ�E������P��y= ͼ�����˶�ʱ�����½��ۣ���BA��DCʼ��ƽ�У���PA��PBʼ����ȣ����ı���PAOB��������ᷢ���仯���ܡ�OBA����������ı���ACEB�����������һ����ȷ����_____������ţ�
ͼ�����˶�ʱ�����½��ۣ���BA��DCʼ��ƽ�У���PA��PBʼ����ȣ����ı���PAOB��������ᷢ���仯���ܡ�OBA����������ı���ACEB�����������һ����ȷ����_____������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�������п���ѧģ���Ծ���ʮ�� ���ͣ���ѡ��
��ͼ�����������ͬ��������ɵļס������������壬���ǵ�����ͼ��һ�µģ�������
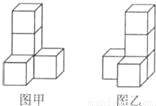
A. ����ͼ B. ����ͼ C. ����ͼ D. ����ͼ
B �����������������������ɿ����״�����������С�����εĸ���Ϊ��3��1���Ҵ�������2��С�����εĸ���Ϊ��1��3�����������⣻ ������ɿ����״�������2��С�����εĸ���Ϊ��3��1���Ҵ�������2��С�����εĸ���Ϊ��3��1���������⣻ ������ɿ����״�������2��С�����εĸ���Ϊ��2��1���Ҵ�������2��С�����εĸ���Ϊ��1��2�����������⣻ ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
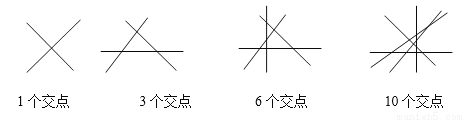
��ͼ������ֱ���ֻཻ��1�����㣬����ֱ���ཻ�����3�����㣬����ֱ���ཻ�����6�����㣬����ֱ���ཻ�����10�����㣬����ֱ���ཻ�����_________�����㣬��ʮ��ֱ���ཻ�����_________�����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
��֪��P��a+1��2a��3������x��ĶԳƵ��ڵ�һ���ޣ���a��ȡֵ��Χ�ǣ�������
A. a����1 B. ��1��a��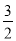 C. ��
C. ��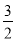 ��a��1 D. a��
��a��1 D. a��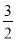
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com