
两个反比例函数y= (k>1)和y=
(k>1)和y= 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y= 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y= 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y= 的图象于点B,BE⊥x轴于点E,当点P在y=
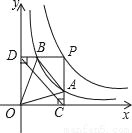
的图象于点B,BE⊥x轴于点E,当点P在y= 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:重庆市长寿区2017-2018学年七年级(上)期中数学 题型:单选题
某种书每本定价8元,若购书不超过10本,按原价付款;若一次购书10本以上,超过10本部分按八折付款.设一次购书数量为x本(x>10),则付款金额为( )
A. 6.4x元 B. (6.4x+80)元 C. (6.4x+16)元 D. (144-6.4x)元
C 【解析】试题解析:有题意可得: 故选C.查看答案和解析>>
科目:初中数学 来源:2017年河北省沧州市中考数学模拟试卷(六) 题型:解答题
解方程组: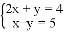
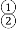 .
.
查看答案和解析>>
科目:初中数学 来源:2017年河北省沧州市中考数学模拟试卷(六) 题型:单选题
互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为( )
A. 120元 B. 100元 C. 80元 D. 60元
C 【解析】【解析】 设该商品的进价为x元/件, 依题意得:(x+20)÷=200,解得:x=80. ∴该商品的进价为80元/件. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年河北省沧州市中考数学模拟试卷(十) 题型:解答题
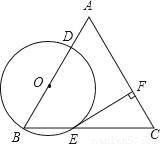
已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:2017年河北省沧州市中考数学模拟试卷(十) 题型:单选题
如图,AB是⊙O的直径,CD是弦,∠BCD=50°,则∠ABD的度数是( )
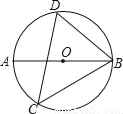
A. 20° B. 25° C. 40° D. 50°
C 【解析】试题解析:连接AD. ∵AB是的直径, 又 故选C.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级12月月考数学试卷 题型:解答题
如图所示是由棱长为1的几个小立方体所组成几何体从上面看到的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体从正面、从左面看到的形状图.并求出此立体图形的表面积。
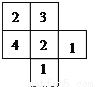
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级12月月考数学试卷 题型:填空题
从一个多边形的某个顶点出发,分别连接这个点和其余各顶点,可以把这个多边形分割成10个三角形,则这个多边形的边数为_____.
12 【解析】根据多边形一个顶点处引出的对角线为n-2个三角形,因此可得到n-2=10,解得n=12,故这个多边形是十二边形. 故答案为:12.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市西湖区绿城育华2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
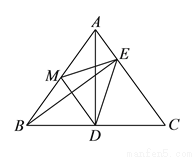
已知:如图,在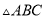 中,
中, 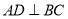 ,垂足为点
,垂足为点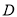 ,
, 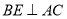 ,垂足为点
,垂足为点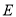 ,
, 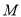 为
为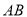 边的中点,连结
边的中点,连结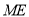 、
、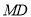 、
、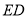 .
.
( )猜想
)猜想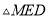 的形状,并说明理由.
的形状,并说明理由.
( )若
)若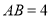 ,
, 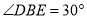 ,求
,求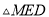 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com