
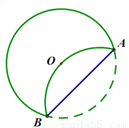
如图,⊙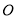 的半径为4.将⊙
的半径为4.将⊙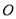 的一部分沿着弦
的一部分沿着弦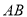 翻折,劣弧恰好经过圆心
翻折,劣弧恰好经过圆心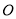 .则折痕AB的长为( )
.则折痕AB的长为( )
A. 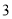 B.
B. 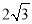 C.
C. 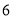 D.
D. 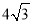
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
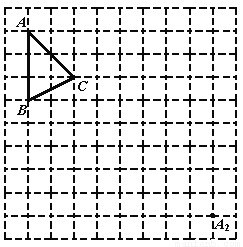
如图,是一个由边长为1的小正方形组成的10×10的正方形网格,
(1)在网格中画出将△ABC向右平移4个单位后的△A1B1C1;
(2)△ABC绕点O旋转180°后,点A与点A2重合,请在网格中画出点O,并画出△ABC绕点O旋转180°后的△A2B2C2;
(3)描述△A1B1C1与△A2B2C2的位置关系是 .
查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:单选题
如图,∠BAC和∠DAE都是直角,∠BAE=108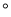 ,则∠DAC的度数为( )
,则∠DAC的度数为( )
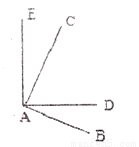
A. 36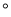 B. 72
B. 72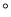 C. 18
C. 18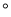 D. 54
D. 54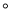
查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:解答题
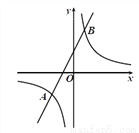
如图,在平面直角坐标系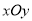 中,一次函数
中,一次函数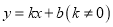 与反比例函数
与反比例函数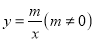 交于点
交于点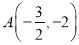 ,
, 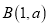 .
.
(1)分别求出反比例函数和一次函数的表达式;
(2)根据函数图象,直接写出不等式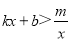 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:填空题
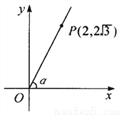
如图,角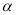 的一边在
的一边在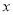 轴上,另一边为射线
轴上,另一边为射线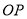 .则
.则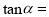 ________________.
________________.
查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:单选题
若反比例函数的图象经过点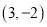 ,则该反比例函数的表达式为( )
,则该反比例函数的表达式为( )
A. 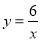 B.
B. 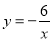 C.
C. 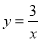 D.
D. 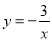
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在边长为6的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则OF的长为_______________.
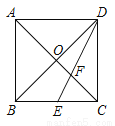
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
若代数式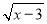 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A. x≥-3 B. x>3 C. x≥3 D. x≤3
C 【解析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可. 【解析】 ∵代数式在实数范围内有意义, ∴x?3≥0, 解得x≥3. 故选C.查看答案和解析>>
科目:初中数学 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:填空题
已知函数的图象经过点(2,1),且与x轴没有交点,写出一个满足题意的函数的表达式__________.
或等,答案不唯一 【解析】一次函数与x轴有交点,反比例函数与x轴无交点,二次函数在满足b2-4ac<0的条件时与x轴无交点,因此满足题意的函数可以是反比例函数或是满足条件的二次函数, 函数的图象经过点(2,1),且与x轴没有交点的函数的表达式可以是: 或等,答案不唯一, 故答案为: 或(答案不唯一).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com