
点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )
A. (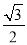 ,
, 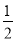 ) B. (-
) B. (-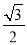 ,-
,- 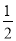 )
)
C. (-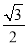 ,
, 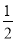 ) D. (-
) D. (-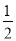 ,-
,- 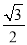 )
)
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
方程x(x-2)= 2 -x的解是( )
A. 2 B. -2,1 C. -1 D. 2,-1
D 【解析】试题分析:∵x(x-2)=2-x ∴x(x-2)+x-2=0 (x-2)(x+1)=0 x-2=0,x+1=0 解得:x1=2,x2=-1 故选D.查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:填空题
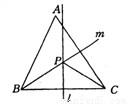
如图所示,在锐角三角形ABC中, 直线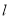 为BC的垂直平分线,直线
为BC的垂直平分线,直线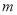 为∠ABC的平分线,
为∠ABC的平分线, 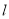 与
与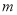 相交于P点.若∠A=600, ∠ACP=240,则∠ABP的度数为_______.
相交于P点.若∠A=600, ∠ACP=240,则∠ABP的度数为_______.
查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:解答题
计算:(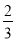 )﹣1+(π﹣3.14)0﹣2sin60°﹣
)﹣1+(π﹣3.14)0﹣2sin60°﹣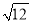 +|1﹣3
+|1﹣3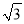 |
|
查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:单选题
如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为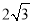 ,则a的值是( )
,则a的值是( )
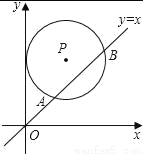
A. 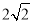 B. 2+
B. 2+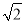 C.
C. 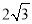 D.
D. 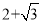
查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:单选题
某红外线遥控器发出的红外线波长为0.000 00094m,用科学计数法表示这个数是( )
A. 9.4×10-7m B. 9.4×107m C. 9.4×10-8m D. 9.4×108m
A 【解析】试题分析:科学计数法是指:a×,且1≤<10,小数点向右移动几位,则n的相反数就是几.查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
如图所示,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,求∠A的度数.
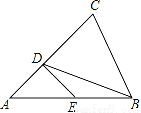
查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )
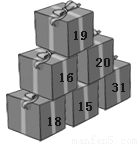
A. 15粒 B. 18粒 C. 20粒 D. 31粒
C 【解析】6个礼包盒一共有糖果:19+16+20+18+15+31=119(粒), (1)119-19=100(粒),因为100÷3=33…1,所以琳琳自己留下的这盒糖果不是19粒; (2)119-16=103(粒),因为103÷3=34…1,所以琳琳自己留下的这盒糖果不是16粒; (3)119-20=99(粒),因为99÷3=33,所以琳琳送给小芬和小红的糖果的总量是9...查看答案和解析>>
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
如图,Rt△ABC中,∠C=90°,∠B=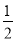 ∠BAC,AD平分∠BAC,若BC=6cm,则CD=_____cm。
∠BAC,AD平分∠BAC,若BC=6cm,则CD=_____cm。
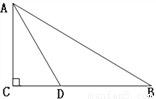
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com