
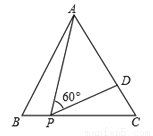
如图,在等边△ABC中,P为BC上一点,D为AC上一点,∠APD=60°,若BP=3,CD=2,求△ABC的边长.
科目:初中数学 来源:江苏省高邮市2017-2018学年八年级12月月考数学试卷 题型:解答题
科目:初中数学 来源:浙江省杭州市西湖区绿城育华2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
对应命题“若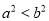 ,则
,则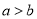 ”,下面四组
”,下面四组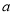 ,
, 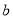 的值中,能说明这个命题是假命题的是( ).
的值中,能说明这个命题是假命题的是( ).
A. 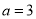 ,
, 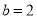 B.
B. 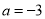 ,
, 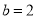 C.
C. 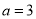 ,
, 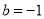 D.
D. 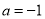 ,
, 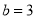
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
已知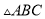 中,
中, 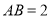 ,
, 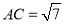 ,
, 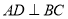 于
于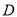 ,
, 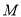 为
为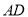 上任一点,则
上任一点,则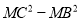 的值为( ).
的值为( ).
A. 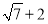 B.
B. 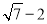 C.
C. 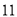 D.
D. 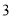
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
一个三角形的两个内角分别为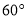 和
和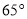 ,这个三角形的外角不可能是( ).
,这个三角形的外角不可能是( ).
A. 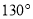 B.
B. 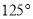 C.
C. 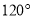 D.
D. 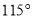
查看答案和解析>>
科目:初中数学 来源:河南省邓州市2018届九年级上学期期中质量评估---数学试卷word版 题型:填空题
如图,已知AB∥CD,E,F分别为AC,BD的中点,若AB=10,CD=6,则EF的长是_______.
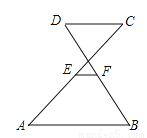
查看答案和解析>>
科目:初中数学 来源:河南省邓州市2018届九年级上学期期中质量评估---数学试卷word版 题型:单选题
如果关于x的一元二次方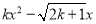 +1=0有两个不相等的实数根,那么k的取值范围是( )
+1=0有两个不相等的实数根,那么k的取值范围是( )
A. -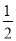 ≤k<
≤k<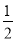 且k≠0 B. k<
且k≠0 B. k<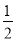 且k≠0
且k≠0
C. -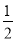 ≤k<
≤k<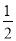 D. k<
D. k<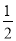
查看答案和解析>>
科目:初中数学 来源:山东省日照市莒县2017-2018学年七年级(上)期中数学试卷 题型:单选题
下列说法:①若a为有理数,则﹣a表示负有理数;②a2=(﹣a)2;③若|a|>b,则a2>b2;④若a+b=0,则a3+b3=0.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】试题解析:①因为a表示有理数,所以a≤0,或a≥0,所以,﹣a并不一定为负有理数,也有可能为非负有理数,故本项推理错误, ②根据幂的乘方运算法则,(﹣a)2=a2,故本项推理正确, ③根据题意,设a=1,b=﹣4,那么|a|>b,但a2>b2并不成立,故本项推理错误, ④由题意可知a=﹣b,所以a3+b3=(﹣b)3+b3=0,故本项推理正确, 所以②④项...查看答案和解析>>
科目:初中数学 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
(10分)感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,易证△ABP∽△PCD,从而得到BP•PC=AB•CD(不需证明)
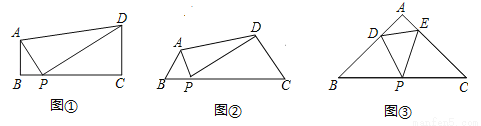
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,结论BP•PC=AB•CD仍成立吗?请说明理由?
拓展:如图③,在△ABC中,点P是BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4 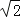 ,CE=3,则DE的长为 .
,CE=3,则DE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com