
若坐标平面上点P(a,1)与点Q(-4,b)关于x轴对称,则( )
A. a=4,b=-1 B. a=-4,b=1 C. a=-4,b=-1 D. a=4,b=l
C 【解析】由题意得 由题意得, a=-4,b=-1 故选C. 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源:吉林省吉林市2016-2017七年级数学上期期末试卷 题型:单选题
用科学记数法表示数6 590 000,结果是( )
A. 6.59×106 B. 65.9×105 C. 0.659×107 D. 6.59×107
A 【解析】【解析】 6 590 000=6.59×106.故选A.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:填空题
若2x2a-5b+ya-3b=0是二元一次方程,则a=______,b=______.
-2 -1 【解析】根据二元一次方程的定义可得x,y的指数都是1, 由二元一次方程定义得: , 故答案为:a=-2,b=-1.查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:填空题
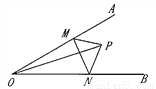
如图所示:∠AOB的内部有一点P,到顶点O的距离为5cm,M、N分别是射线OA、OB上的动点.若∠AOB =30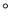 ,则△PMN周长的最小值为________.
,则△PMN周长的最小值为________.
查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB//OC,DC与OB交于点E则∠DEO的度数为( )
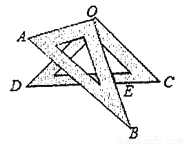
A. 85 B. 70
B. 70 C. 75
C. 75 D. 60
D. 60
查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
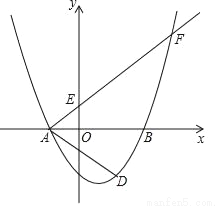
如图,在平面直角坐标系xOy中,已知抛物线y= 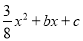 与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且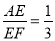 .
.
(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
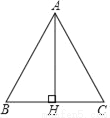
如图,在△ABC中,AB=AC,AH⊥BC,垂足为点H,如果AH=BC,那么sin∠BAC的值是_____.
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:解答题
设函数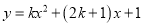 (
(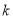 为实数)
为实数)
⑴.写出其中的两个特殊函数,使它们的图象不全是抛物线,并且在同一坐标系中,用描点法画出它们的图像;
⑵.根据所画图像,猜想出:对任意实数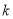 ,函数的图象都具有的特征,并给予证明;
,函数的图象都具有的特征,并给予证明;
⑶.对于任意负实数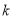 ,当
,当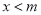 时,
时, 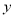 随
随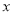 的增大而增大,试求
的增大而增大,试求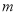 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期九年级期末质量检测数学试卷 题型:单选题
如图,在Rt△ABC和Rt△ABD中,∠ADB=∠ACB=90°,∠BAC=30°,AB=4,AD=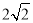 ,连接DC,将Rt△ABC绕点B顺时针旋转一周,则线段DC长的取值范围是
,连接DC,将Rt△ABC绕点B顺时针旋转一周,则线段DC长的取值范围是
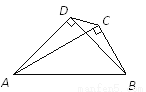
A. 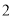 ≤DC≤
≤DC≤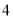 B.
B. 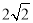 ≤DC≤
≤DC≤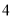
C. 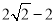 ≤DC≤
≤DC≤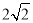 D.
D. 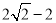 ≤DC≤
≤DC≤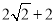
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com