
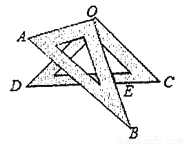
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB//OC,DC与OB交于点E则∠DEO的度数为( )
A. 85 B. 70
B. 70 C. 75
C. 75 D. 60
D. 60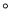
科目:初中数学 来源:吉林省吉林市2016-2017七年级数学上期期末试卷 题型:单选题
当x=-1,y=1时ax+by-3=0,那么当x=1,y=-1时,ax+by-3的值是( )
A. -6 B. 0 C. 6 D. 9
A 【解析】【解析】 ∵当x=﹣1,y=1时,-a+b﹣3=0,即a﹣b=-3,∴当x=1,y=﹣1时,ax+by﹣3=a-b﹣3=﹣3﹣3=﹣6.故选A.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:填空题
若2x5ayb+4与-x1-2by2a是同类项,则b=________.
-2 【解析】本题涉及同类项的概念:所含字母相同,相同字母的指数也相同,由此可得5a=1-2b,b+4=2a,将两式联立组成方程组,解出a,b的值,分别为a=1,b=-2 , 故答案为: b=-2.查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:解答题
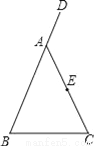
如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:填空题
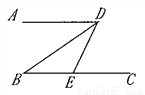
如图,已知AD //BC,∠B=32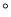 ,DB平分∠ADE,则∠DEC=________.
,DB平分∠ADE,则∠DEC=________.
查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
若坐标平面上点P(a,1)与点Q(-4,b)关于x轴对称,则( )
A. a=4,b=-1 B. a=-4,b=1 C. a=-4,b=-1 D. a=4,b=l
C 【解析】由题意得 由题意得, a=-4,b=-1 故选C.查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
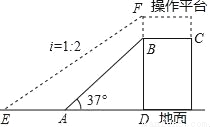
如图,为了将货物装入大型的集装箱卡车,需要利用传送带AB将货物从地面传送到高1.8米(即BD=1.8米)的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.
(1)求传送带AB的长度;
(2)因实际需要,现在操作平台和传送带进行改造,如图中虚线所示,操作平台加高0.2米(即BF=0.2米),传送带与地面所成斜坡的坡度i=1:2.求改造后传送带EF的长度.(精确到0.1米)(参考数值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, 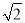 ≈1.41,
≈1.41, 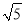 ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:单选题
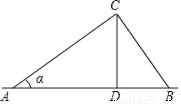
如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )
A. 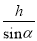 B.
B. 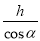 C.
C. 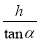 D.
D. 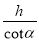
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期九年级期末质量检测数学试卷 题型:填空题
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径为____cm.
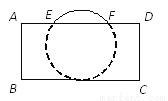
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com