
直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
-7. 【解析】试题分析:点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,则坐标也关于原点对称,即坐标互为相反数,所以可以得到x2+2x=-(x+2),3=-y,所以解得x1=-1,x2=-2.又因点p在第二象限,所以x2+2x<0,所以=-1,故x+2y=-7. 根据题意,得(x2+2x)+(x+2)=0,y=-3.∴x1=-1,x2=-2. ∵点P在第二象限,∴x... 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
下列图形中,阴影部分的面积为2的有( )个.
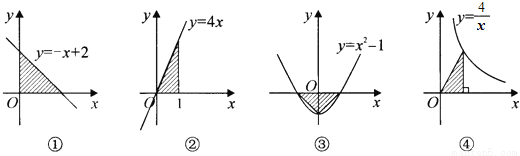
A. 4个 B. 3个 C. 2个 D. 1个
B 【解析】①y=-x+2,当x=0,y=2,当y=0,x=2,∴S阴影部分=12×2×2=2; ②y=4x,当x=1,y=4,∴S阴影部分=12×1×4=2; ③y=x2-1,当x=0,y=-1,当y=0,x=±1, S阴影部分=12×1×2=1; ④y=4x,∴xy=4,∴S阴影部分=12×4=2;故阴影部分的面积为2的有 ①②④.故选B.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:填空题
“比a的2倍小3的数等于a的3倍”可列方程表示为:______.
2a-3=3a 【解析】因为比a的2倍小3的数为:2a-3,a的3倍为:3a,根据题意可列出方程为: 2a-3=3a,故答案为: 2a-3=3a.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:单选题
某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
A. 54-x=20%×108 B. 54-x=20%(108+x)
C. 54+x=20%×162 D. 108-x=20%(54+x)
B 【解析】试题解析:设把x公顷旱地改为林地,根据题意可得方程:54-x=20%(108+x). 故选B.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第23章小结与复习 测试 题型:单选题
已知点P(2+m,n﹣3)与点Q(m,1+n)关于原点对称,则m﹣n的值是( )
A.1 B.﹣1 C.2 D.﹣2
D 【解析】 试题分析:根据关于原点对称的点的横坐标互为相反数,纵坐标互为相反数,可得m、n的值,根据有理数的减法,可得答案. 【解析】 由点P(2+m,n﹣3)与点Q(m,1+n)关于原点对称,得 2+m+m=0,n﹣3+1+n=0. 解得m=﹣1,n=1. m﹣n=﹣1﹣1=﹣2, 故选:D.查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册 第23章 旋转 同步单元检测试卷(Word版附答案) 题型:填空题
如图所示,已知抛物线C1,抛物线C2关于原点中心对称.如果抛物线C1的解析式为y=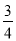 (x+2)2-1,那么抛物线C2的解析式为____________________.
(x+2)2-1,那么抛物线C2的解析式为____________________.
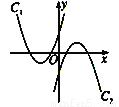
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册 第23章 旋转 同步单元检测试卷(Word版附答案) 题型:单选题
若点A(-2,n)在x轴上,则点B(n-1,n+1)的坐标为 ( )
A. (1,1) B. (-1,-1) C. (1,-1) D. (-1,1)
D 【解析】试题分析:点A(-2,n)在x轴上,所以n=0,所以B点坐标为(-1,1)故选D.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:单选题
图3是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是( )
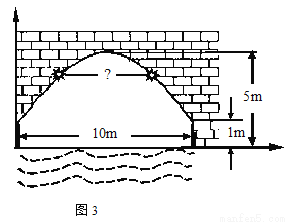
A .3m B.4m C.5m D.6m
C 【解析】试题分析:设距水面1m的水平线为x轴,抛物线两端点中点为原点设立平面直角坐标系, 则抛物线左端点为(-5,0),右端点为(5,0),顶点为(0,4), 设抛物线为: ,将(5,0)代入可得函数解析式为: ; 将y=3代入函数解析式可得: ,则两盏景观灯之间的水平距离为5m,故选择C.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.3二次函数ya(x-h)2+k的图象和性质(3)测试 题型:单选题
要得到抛物线y=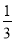 (x﹣4)2,可将抛物线y=
(x﹣4)2,可将抛物线y=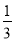 x2( )
x2( )
A. 向上平移4个单位 B. 向下平移4个单位
C. 向右平移4个单位 D. 向左平移4个单位
D 【解析】【解析】 ∵的顶点坐标为(4,0),的顶点坐标为(0,0),∴将抛物线向右平移4个单位,可得到抛物线.故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com