
已知点P(2+m,n﹣3)与点Q(m,1+n)关于原点对称,则m﹣n的值是( )
A.1 B.﹣1 C.2 D.﹣2
D 【解析】 试题分析:根据关于原点对称的点的横坐标互为相反数,纵坐标互为相反数,可得m、n的值,根据有理数的减法,可得答案. 【解析】 由点P(2+m,n﹣3)与点Q(m,1+n)关于原点对称,得 2+m+m=0,n﹣3+1+n=0. 解得m=﹣1,n=1. m﹣n=﹣1﹣1=﹣2, 故选:D.科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:解答题
怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
(1)60;(2)316. 【解析】试题分析:(1)、首先设该店每天卖出A、B两种菜品分别为x、y份,然后根据总营业额和总利润得出二元一次方程组,从而求出答案;(2)、设A种菜品售价降0.5a元,则每天卖(20+a)份,根据每天销售总份数不变,则B种菜品卖(40﹣a)份,每份售价提高0.5a元,然后根据总利润=单件利润×数量得出函数解析式,然后根据二次函数的性质得出最大值. 试题解析:...查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:解答题
A、B两站相距300千米,一列快车从A站开出,行驶速度是每小时60千米,一列慢车从B站开出,行驶速度是每小时40千米,快车先开15分钟,两车相向而行,快车开出几小时后两车相遇?(只列出方程,不用解)
. 【解析】试题分析:等量关系:快车行驶的路程+慢车行驶的路程=两车相距的路程,设快车开出x小时后两车相遇,快车行驶的路程为:60x千米,慢车行驶的路程为:40(x-)千米,根据题意可列出方程. 试题解析:设快车开出x小时后两车相遇, 根据题意得: .查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:单选题
某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“六一”儿童节举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出x支,则依题意可列得的一元一次方程为( )
A. 1.2×0.8x+2×0.9(60+x)=87 B. 1.2×0.8x+2×0.9(60-x)=87
C. 2×0.9x+1.2×0.8(60+x)=87 D. 2×0.9x+1.2×0.8(60-x)=87
B 【解析】【解析】 设该铅笔卖出x支,则圆珠笔卖出(60﹣x)支,由题意得,0.8×1.2x+0.9×2(60﹣x)=87.故选A.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第23章小结与复习 测试 题型:解答题
如图,已知四边形ABCD及点O.求作:四边形A′B′C′D′,使得四边形 与四边形ABCD关于O点中心对称
与四边形ABCD关于O点中心对称
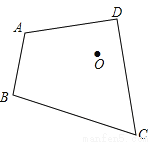
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册 第23章 旋转 同步单元检测试卷(Word版附答案) 题型:解答题
直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
-7. 【解析】试题分析:点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,则坐标也关于原点对称,即坐标互为相反数,所以可以得到x2+2x=-(x+2),3=-y,所以解得x1=-1,x2=-2.又因点p在第二象限,所以x2+2x<0,所以=-1,故x+2y=-7. 根据题意,得(x2+2x)+(x+2)=0,y=-3.∴x1=-1,x2=-2. ∵点P在第二象限,∴x...查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册 第23章 旋转 同步单元检测试卷(Word版附答案) 题型:单选题
如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则图中阴影部分的面积为( )
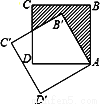
A. 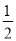 B.
B. 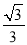 C.
C. 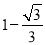 D.
D. 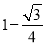
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:填空题
两个数的和为6,这两个数的积最大可以达到____。
9 【解析】试题分析:设其中一个数为x,则另一个数为(6-x),则x(6-x)= ,则这两个数的积最大可以达到9.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.3二次函数ya(x-h)2+k的图象和性质(3)测试 题型:填空题
二次函数y=a(x-h)2+k(a≠0)的顶点坐标是______,对称轴是______,当x=______时,y有最值______;当a>0时,若x______时,y随x增大而减小.
(h,k) 直线x=h h k ≤h. 【解析】【解析】 二次函数y=a(x-h)2+k(a≠0)的顶点坐标是(h,k),对称轴是直线x=h,当x=h时,y有最值k;当a>0时,若x≤h时,y随x增大而减小. 故答案为:(h,k) ; 直线x=h ;h ;k ;≤h.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com