
如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
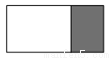
A. 2 cm2 B. 4 cm2 C. 8 cm2 D. 16 cm2
C 【解析】设留下的矩形的宽为x,∵留下的矩形与矩形相似,∴,x=2, ∴留下的矩形的面积为:2×4=8(cm2).故选C.科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
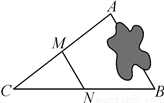
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
【答案】D
【解析】试题分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得MN∥AB,MN=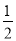 AB,再根据相似三角形的判定解答.
AB,再根据相似三角形的判定解答.
试题解析:∵M、N分别是AC,BC的中点
∴MN∥AB,MN=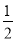 AB,
AB,
∴AB=2MN=2×12=24m
△CMN∽△CAB
∵M是AC的中点
∴CM=MA
∴CM:MA=1:1
故描述错误的是D选项.
故选D.
考点:1.三角形中位线定理;2.相似三角形的应用.
【题型】单选题
【结束】
10
若关于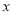 的一元二次方程
的一元二次方程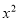 +x-3m=0有两个不相等的实数根,则
+x-3m=0有两个不相等的实数根,则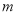 的取值范围是( )
的取值范围是( )
A. 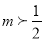 B.
B. 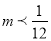 C.
C. 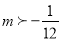 D.
D. 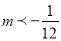
查看答案和解析>>
科目:初中数学 来源:初一数学第一学期5.2.3去分母解一元一次方程 同步练习 题型:解答题
解方程: 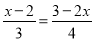 .
.
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
将油箱注满 k 升油后,轿车行驶的总路程S(单位:千米)与平均耗油量 a(单位:升 / 千米)之间是反比例函数关系 S = 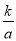 (k 是常数,k≠0).已知某轿车油箱注满油后,以每千米平均耗油 0.1 升的速度行驶,可行驶 500 千米.
(k 是常数,k≠0).已知某轿车油箱注满油后,以每千米平均耗油 0.1 升的速度行驶,可行驶 500 千米.
(1)求该轿车可行驶的总路程 S 与平均耗油量 a 之间的函数解析式(关系式);
(2)当平均耗油量为 0.08 升 / 千米时,该轿车可以行驶多少千米?
(1)s=;(2)625千米 【解析】(1)把a=0.1,S=700代入得: ,解得k=70,∴. (2)把a=0.08代入得:S=875. 故该矫车可以行驶875千米.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:单选题
如图,在△ABC与△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE,连接BD、CE,若AC︰BC=3︰4,则BD︰CE为( )
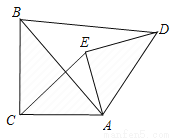
A. 5︰3 B. 4︰3 C. 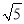 ︰2 D. 2︰
︰2 D. 2︰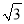
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
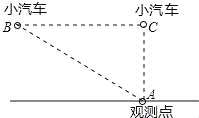
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:填空题
如图,正方形ABCD中,AE⊥BE于E,且AE=3,BE=4,则阴影部分的面积是_______.
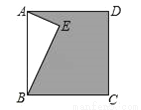
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
如图,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为( )
A. 13 B. 12 C. 7 D. 5
A 【解析】试题分析:根据已知条件可得:BC=BE=5,则AB=DB=17-5=12,根据三角形三边关系可得:12-5<AC<12+5 即7<AC<17,根据直角三角形的性质可得:AC>AB=12,即12<AC<17.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:解答题
如图,已知在⊙O中,AB= 4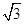 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
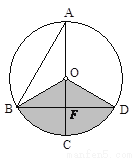
⑴求图中阴影部分的面积;
⑵若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥底面圆的半径.
(1)阴影部分的面积为;(2)这个圆锥底面圆的半径为. 【解析】试题分析:(1)由∠A=30°,可求得∠BOC=60°,再根据垂径定理得∠BOD=120°,由勾股定理得出BF以及OB的长,从而计算出阴影部分的面积即扇形的面积. (2)直接根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得圆锥的底面圆的半径. 试题解析:(1)∵AC⊥BD于F,∠A=30°, ∴∠BOC=60...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com