练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    等腰三角形的两边长是6cm和3cm，那么它的周长是

    A. 9cm B. 12 cm C. 12 cm或15 cm D. 15 cm

    D 【解析】试题分析：题目给出等腰三角形有两条边长为6cm和3cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形． 【解析】 当腰为3cm时，3+3=6，不能构成三角形，因此这种情况不成立． 当腰为6cm时，6﹣3＜6＜6+3，能构成三角形； 此时等腰三角形的周长为6+6+3=15cm． 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山西大学附中2018届九年级10月月考数学试卷 题型：单选题

    “五一”期间，市工会组织篮球比赛，赛制为单循环形式（每两队之间都赛一场），共进行了 45 场比赛，则这次参加比赛的队伍有（ ）

    A. 12 支 B. 11 支 C. 9 支 D. 10 支

    D 【解析】【解析】 设这次有x个队参加比赛，由题意得： x(x-1)=45，解得x=10或﹣9（舍去）； ∴这次有10个队参加比赛．故选D．

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期初二数学期中试卷 题型：填空题

    分式，当时有意义.

    x≠-5 【解析】分式有意义，分母不等于零，所以得x+5≠0，解得x≠?5. 故答案是：x≠?5.

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

    如图，E、A、C三点共线,BC=ED,AB=CE，AC=CD.求证：∠B=∠E

    证明见解析. 【解析】试题分析：首先根据平行线的性质可得∠BAC=∠ECD，再利用AAS定理证明△ACB≌△CED，然后再根据全等三角形对应边相等可得结论． 试题解析：∵AB∥CD， ∴∠BAC=∠ECD， 在△BAC和△ECD中， ， ∴△BAC≌△ECD（SAS）， ∴CB=ED．

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期中考试数学试卷 题型：填空题

    已知直角坐标系中，A（2a-5,7）、B（3，b）关于x轴对称，则式子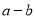的值是__________.

    11 【解析】∵A（2a-5,7）、B（3，b）关于x轴对称， ∴2a-5=3,7=-b,解得a=4,b=-7,a-b=11. 故答案为：11.

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    下列图案是我国几家银行的标志，其中不是轴对称图形的是（ ）

    A. B. C. D.

    B 【解析】试题分析：根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，即可求解． 【解析】 A、C、D都是轴对称图形； B、不是轴对称图形． 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：四川省江县初中2016年秋季八年级期末考试试卷 题型：填空题

    已知x2＋y2＝25，xy＝12，，则x＋y的值为___________

    ±7． 【解析】∵x2＋y2＝25，xy＝12， ∴（x+y）2=x2+2xy+y2=25+2×12=49， ∴x+y=±7．

    查看答案和解析>>

    科目：初中数学 来源：四川省江县初中2016年秋季八年级期末考试试卷 题型：单选题

    下列图形中，是轴对称图形的有（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．由此可得，第1、2、3个图形是轴对称图形，第4个图形不是轴对称图形.故选C.

    查看答案和解析>>

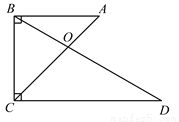
    科目：初中数学 来源：北京市平谷区2018届初三第一学期期末数学试卷 题型：解答题

    如图，∠ABC=∠BCD=90°，∠A=45°，∠D=30°，BC=1，AC，BD交于点O．求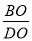的值．

    【解析】试题分析：本题考查了相似三角形的判定与性质，解直角三角形.由∠A=∠ACD，∠AOB=∠COD可证△ABO∽△CDO，从而；再在Rt△ABC和Rt△BCD中分别求出AB和CD的长，代入即可. 【解析】 ∵∠ABC=∠BCD=90°，∴AB∥CD，∴∠A=∠ACD，∴△ABO∽△CDO，∴ ． 在Rt△ABC中，∠ABC=90°，∠A=45°，BC=1，∴AB=1． 在R...

    查看答案和解析>>

    同步练习册答案