练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知直角坐标系中，A（2a-5,7）、B（3，b）关于x轴对称，则式子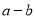的值是__________.

    11 【解析】∵A（2a-5,7）、B（3，b）关于x轴对称， ∴2a-5=3,7=-b,解得a=4,b=-7,a-b=11. 故答案为：11.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山西大学附中2018届九年级10月月考数学试卷 题型：填空题

    某种药品经过两次降价由原来的每盒 12.5 元降到每盒 8 元，如果 2 次降价的百分率相同，设每次降价的百分率为 x，可列出的方程为_____.

    12.5(1-x)2=8 【解析】【解析】 根据题意得：12.5（1﹣x）2=8．故答案为：12.5（1﹣x）2=8．

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期初二数学期中试卷 题型：解答题

    x=1 【解析】试题分析：先把分式方程化为整式方程，求出x的值，代入最简公分母进行检验即可． 试题解析：方程两边同时乘以2x(x+3)，得x+3=4x， 整理，得3x=3， 解得x=1， 当x=1时2x(x+3)≠0， 故x=1是原分式方程的解.

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

    已知：点O到△ABC的两边AB、AC所在直线的距离OD=OE，且OB＝OC.

    （1）如图，若点O在BC上，求证：AB＝AC；

    （2）如图，若点O在△ABC的内部，求证：AB＝AC；

    （3）若点O在△ABC的外部，AB＝AC成立吗？请画图表示.

    （1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）求证AB=AC，就是求证∠B=∠C，可通过构建全等三角形来求．过点O分别作OE⊥AB于E，OF⊥AC于F，那么可以用斜边直角边定理（HL）证明Rt△OEB≌Rt△OFC来实现；（2）首先得出Rt△OEB≌Rt△OFC，进而得出AB=AC；（3）不一定成立，当∠A的平分线所在直线与边BC的垂直平分线重合时，有AB=AC；否则，AB≠...

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

    如图，已知△ABC的三个顶点分别为A（2，3）、B（3，1）、C（－2，－2）.

    （1）请在图中作出△ABC关于y轴对称图形△DEF（A、B、C的对应点分别是D、E、F），并直写出D、E、F的坐标.D、E、F点的坐标是：D( , ) E( , ) F( , )；

    （2）求四边形ABED的面积.

    答案见解析. 【解析】试题分析：（1）分别画出A、B、C三点关于y轴的对称点D、E、F即可解决问题． （2）四边形ABED是等腰梯形，根据梯形的面积公式即可解决问题． 试题解析：(1)△ABC关于y轴的轴对称图形△DEF如图所示， 由图象可知：D(?2,3)、E(?3,1)、F(2,?2)， (2)S梯形ABED=×(4+6) ×2=10.

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    等腰三角形的两边长是6cm和3cm，那么它的周长是

    A. 9cm B. 12 cm C. 12 cm或15 cm D. 15 cm

    D 【解析】试题分析：题目给出等腰三角形有两条边长为6cm和3cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形． 【解析】 当腰为3cm时，3+3=6，不能构成三角形，因此这种情况不成立． 当腰为6cm时，6﹣3＜6＜6+3，能构成三角形； 此时等腰三角形的周长为6+6+3=15cm． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：四川省江县初中2016年秋季八年级期末考试试卷 题型：解答题

    （1）如图，∠A=∠D=90°，BE平分∠ABC，且点E是AD的中点，求证：BC=AB+CD．

    （2）如图，△ACB和△ECD都是等边三角形，点A、D、E在同一直线上，连接BE．

    ①求证：AD=BE；

    ②求∠AEB的度数．

    （1）证明见解析；（2）①证明见解析；②60°． 【解析】试题分析：（1）过点E作EF⊥BC于点F，可得∠EFB=∠A=90°，已知BE平分∠ABC，根据角平分线的定义可得∠ABE=∠FBE，利用AAS即可判定ΔABE≌ΔFBE，根据全等三角形的性质可得AE=EF，AB=BF，又由点E是AD的中点，可得AE=ED=EF，再利用HL判定RtΔCDE≌RtΔCFE，即可得CD=CF，所以BC=C...

    查看答案和解析>>

    科目：初中数学 来源：四川省江县初中2016年秋季八年级期末考试试卷 题型：单选题

    如图，AB=AC，CF⊥AB于F，BE⊥AC于E，CF与BE交于点D．有下列结论：

    ①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上；④点C在AB的中垂线上．

    以上结论正确的有（　　）个．

    A. 1 B. 2 C. 3 D. 4

    C 【解析】∵BE⊥AC，CF⊥AB， ∴∠AEB=∠AFC=∠CED=∠DFB=90°． 在△ABE和△ACF中， ， ∴△ABE≌△ACF（AAS）， ∴AE=AF． ∵AC=AB， ∴CE=BF． 在△CDE和△BDF中， ， ∴△CDE≌△BDF（AAS） ∴DE=DF． ∵BE⊥AC于E，CF⊥AB， ∴...

    查看答案和解析>>

    科目：初中数学 来源：北京市平谷区2018届初三第一学期期末数学试卷 题型：解答题

    如图，点C是以AB为直径的⊙O上一动点，过点C作⊙O直径CD，过点B作BE⊥CD于点E．已知AB=6cm，设弦AC的长为xcm，B，E两点间的距离为ycm（当点C与点A或点B重合时，y的值为0）．

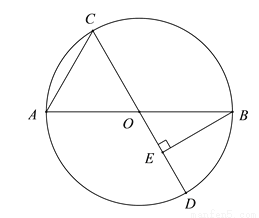
    小冬根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

    下面是小冬的探究过程，请补充完整：

    （1）通过取点、画图、测量，得到了x与y的几组值，如下表：

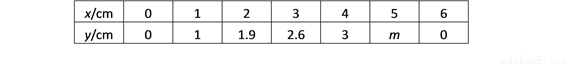
    经测量m的值是（保留一位小数）．

    （2）建立平面直角坐标系，描出表格中所有各对对应值为坐标的点，画出该函数的图象；

    （3）在（2）的条件下，当函数图象与直线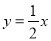相交时（原点除外），∠BAC的度数是_____．

    （1）m=2.76；（2）答案见解析；（3）答案见解析，30°． 【解析】试题分析：（1）根据当AC=5cm时，测量出m的值即可；（2）用描点法画出该函数的图像；（3）由图像可得BE=2.6，AC=5.2，根据∠BOC的正弦值求得∠BOC=60°，再由圆周角定理可得∠BAC =30°． 【解析】 （1）m=2.76； （2）如图； （3）如图, 当函数图象与直线相交时,B...

    查看答案和解析>>

    同步练习册答案