练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若a＞0，b＜﹣2，则点（a，b+2）在（ ）

    A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

    D 【解析】试题分析：应先判断出所求的点的横纵坐标的符号，进而判断点所在的象限． 【解析】 ∵a＞0，b＜﹣2， ∴b+2＜0， ∴点（a，b+2）在第四象限．故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：解答题

    问题探究：

    新定义：

    将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”，其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”（例如圆的直径就是圆的“等积线段”）

    解决问题：

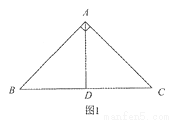
    已知在Rt△ABC中，∠BAC=90°，AB=AC=2.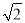

    （1）如图1，若AD⊥BC，垂足为D，则AD是△ABC的一条等积线段，直接写出AD的长；

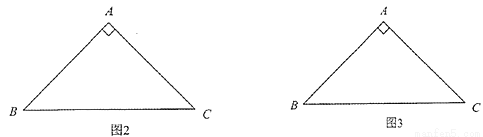
    （2）在图2和图3中，分别画出一条等积线段，并直接写出它们的长度. （要求：图1、图2和图3中的等积线段的长度各不相等）

    （1）AD=2；（2）符合题意的图形见解析，BE=，GH=2 【解析】试题分析：（1）根据等腰直角三角形的性质，底边上的高线即可求得； （2）作中线BE，中线BE即为一条等积线，利用勾股定理即可求得长度； 作GH//BC，GH将Rt△ABC的面积分为相等的两份，则GH即为一条等积线，根据相似三角形的性质即可求得长度. 试题解析：（1）在Rt△ADC中， ∵AC=2，∠...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：单选题

    抛物线y=ax2+bx+c（a≠0）的图象如图所示，则下列说法正确的是（　　）

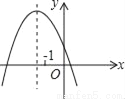
    A. b2﹣4ac＜0 B. abc＜0 C. 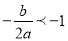D. a﹣b+c＜0

    C 【解析】抛物线开口向下，所以，对称轴在-1的左侧，所以，抛物线与横轴有两个交点，说明b2﹣4ac大于0，C正确，故选C

    查看答案和解析>>

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：填空题

    如图，在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻，当甲带球冲到A点时，乙也跟随冲到B点．从数学角度看，此时甲是自己射门好，还是将球传给乙，让乙射门好？

    答________________.

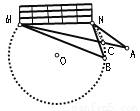
    乙射门好 【解析】 试题解析：∵∠MBN=∠MCN， 而∠MCN＞∠A， ∴∠MBN＞∠A， ∴从数学角度看，此时甲将球传给乙，让乙射门好．

    查看答案和解析>>

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：单选题

    在Rt△ABC中，∠Ｃ＝90°,AC=3cm,BC=4cm.给出下列三个结论:

    ① 以点C为圆心,2.3cm长为半径的圆与AB相离;

    ② 以点C为圆心,2.4cm长为半径的圆与AB相切;

    ③ 以点C为圆心,2.5cm长为半径的圆与AB相交;则上述结论中正确的个数是（ ）

    A.0个 B.1个 C.2个 D.3个

    D 【解析】此题是判断直线和圆的位置关系，需要求得直角三角形斜边上的高．先过C作CD⊥AB于D，根据勾股定理得AB=5，再根据直角三角形的面积公式，求得CD=2.4．①，即d＞r，直线和圆相离，正确；②，即d=r，直线和圆相切，正确；③，d＜r，直线和圆相交，正确．共有3个正确． 【解析】 ①，d＞r，直线和圆相离，正确； ②，d=r，直线和圆相切，正确； ③，d＜r，直线和圆相...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省随州市中考数学模拟试卷 题型：解答题

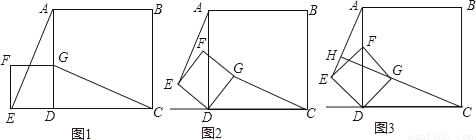
    （1）如图1，正方形ABCD和正方形DEFG，G在AD边上，E在CD的延长线上．求证：AE=CG，AE⊥CG；

    （2）如图2，若将图1中的正方形DEFG绕点D顺时针旋转角度θ（0°＜θ＜90°），此时AE=CG还成立吗？若成立，请给予证明；若不成立，请说明理由；

    （3）如图3，当正方形DEFG绕点D顺时针旋转45°时，延长CG交AE于点H，当AD=4，DG=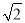时，求线段CH的长．

    （1）（2）见解析；（3）． 【解析】试题分析：（1）先判断出△ADE≌△CDG，然后用互余判断出垂直； （2）先判断出△ADE≌△CDG，然后用互余判断出垂直； （3）先判断出△ADE≌△CDG，然后用互余判断出垂直，然后用勾股定理计算出CM，AM最后用相似即可． 试题解析：（1）在△ADE和△CDG中， DE=DG，∠ADE=∠CDG，AD=CD， ∴△AD...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省随州市中考数学模拟试卷 题型：填空题

    如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为______．

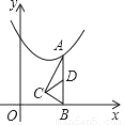
    1. 【解析】试题分析：根据题意可知，当A点在抛物线的顶点（1，2）时，AB的长最短，最短为2，这时根据直角三角形斜边上的中线等于斜边的一半，可直接求解为CD=1. 故答案为：1.

    查看答案和解析>>

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：解答题

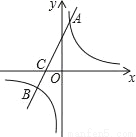
    如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=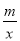（m≠0）的图象交于A、B两点，与x轴交于C点，点A的坐标为（n，6），点C的坐标为（﹣2，0），且tan∠ACO=2．

    （1）求该反比例函数和一次函数的解析式；

    （2）求点B的坐标．

    （1）反比例函数的解析式为，一次函数的解析式为y=2x+4；（2）点B坐标为（﹣3，﹣2）. 【解析】试题分析：（1）先过点A作AD⊥x轴，根据tan∠ACO=2，求得点A的坐标，进而根据待定系数法计算两个函数解析式；（2）先联立两个函数解析式，再通过解方程求得交点B的坐标即可． 试题解析：（1）过点A作AD⊥x轴，垂足为D．由A（n，6），C（﹣2，0）可得，OD=n，AD=6，CO...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学二模试卷 题型：单选题

    二次函数y=ax2+bx+c的图象如下图所示，则一次函数y=bx+b2-4ac与反比例函数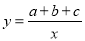在同一坐标系内的图象大致为（ ）

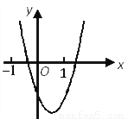
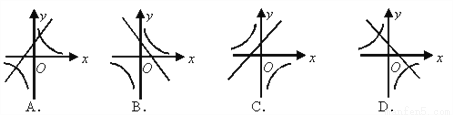
    A. （A） B. （B） C. （C） D. （D）

    D 【解析】观察二次函数图象可知开口方向向上，对称轴直线x＝－ ＞0，当x＝1时y＝a＋b＋c＜0，∴a>0，b<0，∴一次函数y＝bx＋a的图象经过第一、二、四象限，反比例函数y＝ 的图象在第二、四象限，只有D选项图象符合．故选D.

    查看答案和解析>>

    同步练习册答案