练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    有3cm，3cm，6cm，6cm，12cm，12cm的六条线段，任选其中的三条线段组成一个等腰三角形，则最多能组成等腰三角形的个数为（　　）

    A. 1                                            B. 2                                            C. 3                                            D. 4

    C 【解析】根据等腰三角形的性质和三边关系可得:3,6,6,和3,12,12,和6,12,12,三组可以构成等腰直角三角形,故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：黄金30题系列 八年级数学 大题好拿分 题型：解答题

    已知：a，b，c分别为△ABC的三条边的长度，请用所学知识说明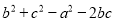： 是正数、负数或零。

    见解析 【解析】试题分析：根据三角形三边关系可知b﹣（a+c）＜0，a+b﹣c＞0，再由所给的式子进行因式分解可以整体代入判断出结果. 试题解析：根据三角形的三边关系，得b﹣（a+c）＜0，a+b﹣c＞0， ∴==（b﹣c﹣a）（b﹣c+a）＜0， 即是负数．

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（三） 题型：单选题

    一个等腰三角形的两边长分别是方程x2－7x＋10＝0的两根，则该等腰三角形的周长是(　　)

    A. 12 B. 9 C. 13 D. 12或9

    A 【解析】试题分析：因式分解可得：(x－2)(x－5)=0，解得： =2， =5.当2为底，5为腰时，则三角形的周长为12；当5为底，2为腰时，则无法构成三角形.

    查看答案和解析>>

    科目：初中数学 来源：湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷（含答案） 题型：填空题

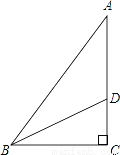
    如图，在Rt△ABC中，∠C=90°，BD是三角形的角平分线，交AC于点D，AD=2.2cm，AC=3.7cm，则点D到AB边的距离是________ cm．

    1.5 【解析】根据角平分线的性质可得:点D到AB的距离等于点D到BC的距离,所以点D到AB边的距离等于CD=AC－AD=3.7－2.2=1.5,故答案为:1.5.

    查看答案和解析>>

    科目：初中数学 来源：湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷（含答案） 题型：单选题

    一次数学课上，老师请同学们在一张长为18厘米，宽为16厘米的矩形纸板上，剪下一个腰长为10厘米的等腰三角形，且要求等腰三角形的一个顶点与矩形的一个顶点重合，其它两个顶点在矩形的边上，则剪下的等腰三角形的面积为 ( )平方厘米。

    A. 50 B. 50或40 C. 50或40或30 D. 50或30或20

    C 【解析】试题解析：如图四边形ABCD是矩形， 本题可分三种情况： 如图(1):△AEF中， ②如图(2):△AGH中， 在中， 根据勾股定理有： ③如图(3):△AMN中， 在中， 根据勾股定理有： 故选C.

    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年八年级（上）期末复习测试数学试卷 题型：解答题

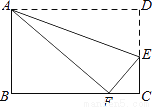
    如图，将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上F点处，已知CE=6cm，AB=16cm，求BF的长．

    12cm 【解析】试题分析：由折叠和矩形性质可知：AF=AD=BC，EF=DE，AB=DC，由已知数据可求出FC，设BF为x，AF就是CF+x，AB已给出，在Rt△ABF中，利用勾股定理即可求出BF长． 试题解析：由题意可知△ADE≌△AFE，在矩形ABCD中，CD=AB=16，AD=CB，，∵CE=6∴．在Rt△中，，设BF=x，则，∴．在△中，， 即，解得: x=12．即BF=12...

    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年八年级（上）期末复习测试数学试卷 题型：填空题

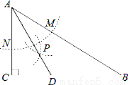
    如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法①AD是∠BAC的平分线；②∠ADC=60°③点D在AB的中垂线上；正确的个数是 个．

    3． 【解析】 试题分析：根据角平分线的作法可知①正确，在△ABC中，∠C=90°，∠B=30°可得∠CAB=60°，由①得，∠CAD=∠BAD=∠CAB=30°，所以∠ADC=∠BAD+∠B=60°；又因∠BAD=∠B=30°，所以AD=BD，根据线段垂直平分线的性质可得点D在AB的中垂线上，即本题的结论正确的有3个．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：解答题

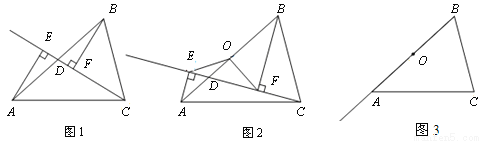
    已知点D是△ABC边AB上一动点（不与A，B重合）分别过点A，B向直线CD作垂线，垂足分别为E，F，O为边AB的中点.

    （1）如图1，当点D与点O重合时，AE与BF的位置关系是____________，OE与OF的数量关系是__________；

    （2）如图2，当点D在线段AB上不与点O重合时，试判断OE与OF的数量关系，并给予证明；

    （3）如图3，当点D在线段BA的延长线上时，此时（2）中的结论是否成立？请画出图形并写出主要证明思路．

    AE∥BF，OE=OF． OE=OF． 【解析】试题分析：（1）根据AAS推出△AEQ≌△BFQ，推出AE=BF即可； （2）延长EQ交BF于D，求出△AEQ≌△BDQ，根据全等三角形的性质得出EQ=QD，根据直角三角形斜边上中点性质得出即可； （3）延长EQ交FB于D，求出△AEQ≌△BDQ，根据全等三角形的性质得出EQ=QD，根据直角三角形斜边上中点性质得出即可． 试题...

    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市路北区2017-2018学年七年级（上）期末复习数学试卷 题型：单选题

    钟表上2时25分时，时针与分针所成的角是(    )

    A. 77.5 ° B. 77 °5′ C. 75° D. 以上答案都不对

    A 【解析】如下图所示，钟表上2时25分，时针指向2，分针指向5，每相邻两个数字之间的夹角为30°，25分即小时，则表的时针与分针在2时25分时夹角是： ，故选A.

    查看答案和解析>>

    同步练习册答案