
如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).当△ADE的一边与△ABC的某一边平行(不共线)时,写出旋转角α的所有可能的度数为 .
 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:单选题
用反证法证明:“若整数系数一元二次方程ax2+bx+c=0(a≠0)有有理根,则a,b,c中至少有一个是偶数”,下列假设中正确的是( )
A. 假设a,b,c都是偶数 B. 假设a,b,c都不是偶数
C. 假设a,b,c至多有一个是偶数 D. 假设a,b,c至多有两个是偶数
B 【解析】假设a,b,c都不是偶数,故选B.查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
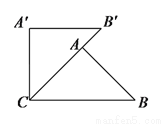
如图,在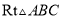 中,
中, 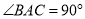 ,将
,将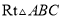 绕点
绕点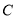 按逆时针方向逆转
按逆时针方向逆转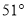 ,得到
,得到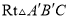 ,点
,点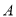 在边
在边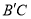 上,则
上,则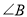 的大小为( ).
的大小为( ).
A. 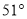 B.
B. 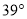 C.
C. 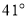 D.
D. 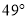
查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:单选题
二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
⑴ac<0;
⑵当x>1时,y的值随x值的增大而减小.
⑶3是方程ax2+(b﹣1)x+c=0的一个根;
⑷当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
B 【解析】二次函数过(-1,-1),(0,3),(1,5), , 解得,y=-.对称轴,, (1)正确,(2)开口向下,对称轴,x>1时y先增大再减小,错误,(3)+2,解得, .正确,(4)+2,所以由(3)得到函数与x轴的交点,作图知,﹣1<x<3时,y>0正确. 所以(1)(3)(4)正确.选B.查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:单选题
已知,如图,下列条件中,不能判断直线a∥b的是( )
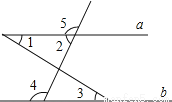
A. ∠1=∠3 B. ∠2=∠3 C. ∠4=∠5 D. ∠2+∠4=180º
B 【解析】当∠1=∠3时,a∥b; 当∠4=∠5时,a∥b; 当∠2+∠4=180°时,a∥b. 故选B.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:填空题
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是直线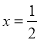 ;④在对称轴左侧,y随x增大而增大.从上表可知,以上说法中正确的是____________.(填写序号)
;④在对称轴左侧,y随x增大而增大.从上表可知,以上说法中正确的是____________.(填写序号)
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:填空题
已知m为实数,若(m2+4m)2+5(m2+4m)﹣24=0,则m2+4m的值为 .
3或﹣8. 【解析】 试题分析:设t=m2+4m,则原方程转化为关于t的一元二次方程t2+5t﹣24=0,利用因式分解法求得t的值,即m2+4m的值即可. 【解析】 设t=m2+4m,则由原方程得到:t2+5t﹣24=0, 整理,得 (t﹣3)(t+8)=0, 解得t=3或t=﹣8. 故答案是: 3或﹣8.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
如图,BD是⊙O的直径,点A、C在⊙O上,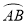 =
=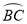 ,∠AOB=60°,则∠BDC的度数是( ).
,∠AOB=60°,则∠BDC的度数是( ).
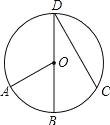
A.60° B.45° C.35° D.30°
D. 【解析】 试题分析:直接根据圆周角定理求解.连结OC,如图,∵=,∴∠BDC=∠BOC=∠AOB=×60°=30°. 故选:D.查看答案和解析>>
科目:初中数学 来源:2017年广东省东莞市堂星晨学校考数学模拟试卷 题型:单选题
如图为二次函数y=ax2+bx+c (a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④ 当-1<x<3时,y>0 其中正确的个数为()
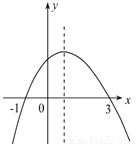
A. 1 B. 2 C. 3 D. 4
C 【解析】试题分析:①由二次函数y=ax2+bx+c(a≠0)的开口向下,可知a<0,故错误; ②由二次函数与x轴的交点的坐标为(-1,0),(3,0),可知对称轴为x==1,即-=1, 因此可得b=-2a,即2a+b=0,故正确; ③由函数的顶点在第一象限,因此可知,当x=1时,y=a+b+c>0,故正确; ④由二次函数与x轴的交点的坐标为(-1,0),(3,0)...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com