
如图,数轴上A、B、C三点表示的数分别为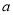 、
、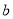 、
、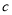 ,且
,且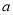 、
、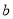 满足
满足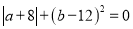 .
.

(1)则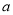 = ,
= , 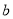 = ;
= ;
(2)动点P从A点出发,以每秒10个单位的速度沿数轴向右运动,到达B点停留片刻后立即以每秒6个单位的速度沿数轴返回到A点,共用了6秒;其中从C到B,返回时从B到C(包括在B点停留的时间)共用了2秒.
①求C点表示的数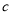 ;
;
②设运动时间为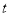 秒,求
秒,求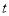 为何值时,点P到A、B、C三点的距离之和为23个单位?
为何值时,点P到A、B、C三点的距离之和为23个单位?
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,点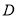 在⊙
在⊙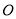 的直径
的直径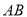 的延长线上,点
的延长线上,点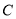 在⊙
在⊙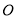 上,
上, 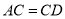 ,
, 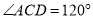 .
.
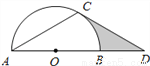
(1)求证: 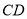 是⊙
是⊙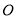 的切线;
的切线;
(2)若⊙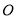 的半径为
的半径为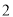 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:填空题
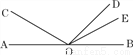
如图,图中的角总共有____________个.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:填空题
在平面直角坐标系中,将抛物线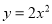 向上平移3个单位,得到的抛物线的函数表达式为 .
向上平移3个单位,得到的抛物线的函数表达式为 .
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:单选题
如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:FB等于 ( )
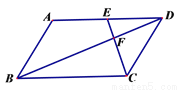
A. 1∶1 B. 1∶2 C. 1∶3 D. 2∶3
B 【解析】∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC, ∴△DEF∽△BCF, ∴DE:BC=DF:BF, ∵点E是边AD的中点, ∴DE:BC=1:2, ∴DF:BF=1:2, 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
七年级(2)班举行元旦晚会,打算买一些糖果分给班级的同学,如果每人分3颗,那么余15颗;如果每人分4颗,那么就少30颗. ?(先在横线上提出一个问题把题目补充完整,然后解答)
提出问题(答案不唯一); 解答见解析. 【解析】试题分析:设共有x位同学,根据两种分法的糖果数量相同可得出方程,从而解出即可. 试题解析:提出的问题是:这个班共有多少同学. 解答如下: 设共有x位同学,则 2x+20=3x-30, 解得x=50. 答:共有50位同学.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
如图,直线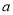 、
、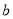 相交于点
相交于点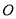 ,将量角器的中心与点
,将量角器的中心与点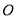 重合,发现表示
重合,发现表示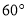 的点在直线
的点在直线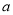 上,表示
上,表示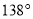 的点在直线
的点在直线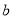 上,则
上,则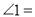 _________
_________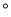 .
.
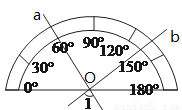
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
在△ABC中,AB=AC,点D为BC中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:DE=DF
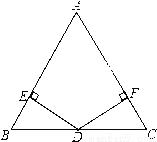
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
已知在平面直角坐标系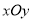 中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
(1)当⊙O的半径为1时:
①点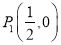 ,
,  ,
, 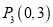 中,⊙O的关联点有_____________________.
中,⊙O的关联点有_____________________.
②直线经过(0,1)点,且与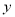 轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标
轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标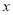 的取值范围.
的取值范围.
(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径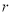 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com