练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是(　　)

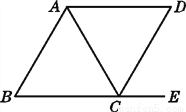
    A. AD∥BC B. AB∥CD

    C. CA平分∠BCD D. AC平分∠BAD

    B 【解析】由CD为角平分线，得到∠ACD=∠ECD，根据已知∠B=∠ACD，等量代换得到一对同位角∠ECD=∠B，利用同位角相等两直线平行即可得AB∥CD， 故选：B.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级下册 2.2 探索直线平行的条件（1） 同步练习 题型：填空题

    如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为__________,理由是_________. 

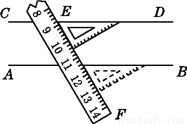
    AB∥CD; 同位角相等,两直线平行 【解析】根据题意，∠1与∠2是三角尺的同一个角，所以∠1=∠2，所以，AB∥CD（同位角相等，两直线平行）. 故答案为：AB∥CD；同位角相等，两直线平行.

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：填空题

    一位运动员投掷铅球，如果铅球运行时离地面的高度为y（米）关于水平距离x（米）的函数解析式为y=﹣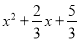，那么铅球运动过程中最高点离地面的距离为________米．

    3 【解析】由题意可得：y=﹣=? (x2?x)+ =? (x?)2+， 故铅球运动过程中最高点离地面的距离为： m. 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：单选题

    二次函数y=-x2+2x+2化为y=a（x-h）2+k的形式，下列正确的是( )

    A. y=-（x-1）2+2 B. y=-（x-1）2+3 C. y=（x-2）2+2 D. y=（x-2）2+4

    B 【解析】解决本题的关键是使用配方法，可得顶点式函数解析式. 【解析】 y=x2-2x+4配方，得 y=（x-1）2+3， 故选B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：单选题

    某人在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来相同，这两次拐弯的角度可能是（ ）

    A. 第一次左拐30°，第二次右拐30°

    B. 第一次右拐50°，第二次左拐130°

    C. 第一次右拐50°，第二次右拐130°

    D. 第一次向左拐50°，第二次向左拐120°

    A 【解析】试题解析：如图： 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：单选题

    如图，在所标识的角中，同位角是（　　）

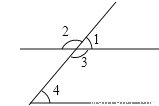
    A. ∠1和∠2 B. ∠1和∠3 C. ∠1和∠4 D. ∠2和∠3

    C 【解析】试题解析：根据同位角、邻补角、对顶角的定义进行判断， A、∠1和∠2是邻补角，故A错误； B、∠1和∠3是邻补角，故B错误； C、∠1和∠4是同位角，故C正确； D、∠2和∠3是对顶角，故D错误． 故选C． 考点:同位角、内错角、同旁内角．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：解答题

    如图，在△ABC中，AD=DB，∠1=∠2.求证：△ABC∽△EAD.

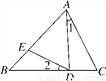
    证明见解析. 【解析】试题分析:先根据等边对等角可得: ∠B=∠BAD,继而可得:∠C=∠ADE,利用两角相等可判定两三角形相似. 试题解析:∵AD=DB, ∴∠B=∠BAD, ∵∠BDA=∠1+∠C=∠2+∠ADE, ∴∠C=∠ADE, ∴△ABC∽△EAD.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：单选题

    如图，菱形ABCD的周长为8cm，高AE长为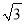cm，则对角线AC长和BD长之比为（　　）

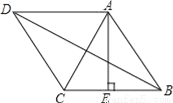
    A. 1：2 B. 1：3 C. 1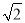： D. 1：

    D 【解析】试题解析：如图，设AC，BD相较于点O， ∵菱形ABCD的周长为8cm， ∴AB=BC=2cm， ∵高AE长为cm， ∴BE==1（cm）， ∴CE=BE=1cm， ∴AC=AB=2cm， ∵OA=1cm，AC⊥BD， ∴OB==（cm）， ∴BD=2OB=2cm， ∴AC：BD=1： ． 故选D．

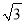
    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：期中检测卷 题型：填空题

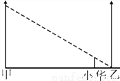
    甲、乙两盏路灯底部间的距离是30米，一天晚上，当小华走到距路灯乙底部5米处时，发现自己的身影顶部正好接触路灯乙的底部．已知小华的身高为1.5米，那么路灯甲的高为_____米．

    9 【解析】如图，设路灯甲的高为米，由题意和图可得： ，解得， ∴路灯甲的高为9米.

    查看答案和解析>>

    同步练习册答案