
解方程:
(1)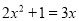 (配方法)
(配方法)
(2)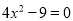 (因式分解法)
(因式分解法)
(3)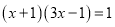 ( 公式法)
( 公式法)
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:填空题
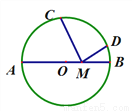
如图,AB是⊙O的直径,已知AB=2,C,D是⊙O的上的两点,且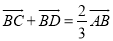 ,M是AB上一点,则MC+MD的最小值是__________.
,M是AB上一点,则MC+MD的最小值是__________.
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
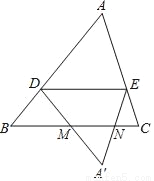
如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
(1)求证:DB=DM.
(2)若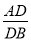 =2,DE=6,求线段MN的长.
=2,DE=6,求线段MN的长.
(3)若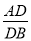 =n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
=n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:单选题
方程x2﹣6x+4=0的根的情况是( )
A. 没有实数根 B. 只有一个实数根
C. 有两个相等的实数根 D. 有两个不相等的实数根
D 【解析】在方程x2?6x+4=0中,△=(?6)2?4×1×4=20>0, ∴方程x2?6x+4=0有两个不相等的实数根. 故选:D.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
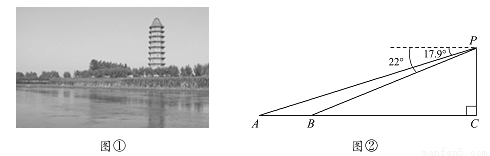
如图,耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图①),数学兴趣小组的小亮同学在塔上观景点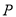 处,利用测角仪测得运河两岸上的
处,利用测角仪测得运河两岸上的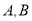 两点的俯角分别为
两点的俯角分别为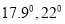 ,并测得塔底点
,并测得塔底点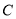 到点
到点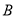 的距离为
的距离为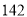 米(
米(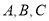 在同一直线上,如图②)求运河两岸的
在同一直线上,如图②)求运河两岸的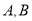 两点的距离(精确到1米)
两点的距离(精确到1米)
(参考数据: 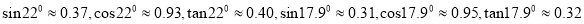 )
)
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:填空题
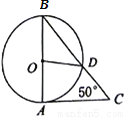
如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,连接BC交⊙O于点D,若∠C=50°,则∠AOD=__°.
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:单选题
如图,为测楼房BC的高,在距离楼房30米的A处测得楼顶的仰角为α,则楼高BC为( )

A.30tanα米
B.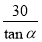 米
米
C.30sinα米
D.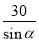 米
米
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:填空题
一元二次方程x2﹣4x=0的解是_____.
x1=0,x2=4. 【解析】x2﹣4x=0, x(x-4)=0, x1=0,x2=4. 故答案为x1=0,x2=4.查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
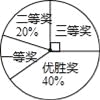
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com