
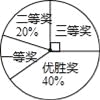
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
解方程:
(1)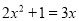 (配方法)
(配方法)
(2)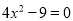 (因式分解法)
(因式分解法)
(3)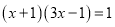 ( 公式法)
( 公式法)
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:解答题
在平面直角坐标系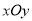 中,抛物线
中,抛物线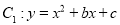 经过点
经过点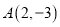 ,且与
,且与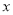 轴的一个交点为
轴的一个交点为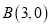 .
.
(1)求抛物线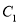 的表达式;
的表达式;
(2)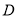 是抛物线
是抛物线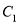 与
与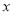 轴的另一个交点,点
轴的另一个交点,点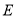 的坐标为
的坐标为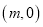 ,其中
,其中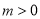 ,△
,△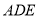 的面积为
的面积为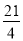 .
.
①求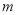 的值;
的值;
②将抛物线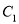 向上平移
向上平移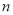 个单位,得到抛物线
个单位,得到抛物线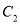 .若当
.若当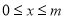 时,抛物线
时,抛物线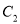 与
与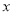 轴只有一个公共点,结合函数的图象,求
轴只有一个公共点,结合函数的图象,求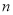 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:填空题
埃是表示极小长度的单位名称,是为纪念瑞典物理学家埃基特朗而定的.1埃等于一亿分之一厘米,请用科学记数法表示1埃等于___________厘米.
1×10-8 【解析】试题分析:此题考的是科学记数法: 由科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.因此1埃=厘米.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:单选题
下列电视台的台标,是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:填空题
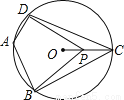
如图,四边形ABCD内接于⊙O,∠DAB=120°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为______度(写出一个即可).
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:单选题
如图,在方格纸上△DEF是由△ABC绕定点P顺时针旋转得到的.如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,那么点P的位置为( )
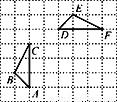
A. (5,2) B. (2,5) C. (2,1) D. (1,2)
A 【解析】如图,分别连接AD、CF, 然后作它们的垂直平分线,它们交于P点,则它们旋转中心为P, 根据图形知道△ABC绕P点顺时针旋转90°得到△DEF, ∴P的坐标为(5,2). 故选A.查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:填空题
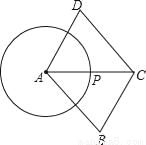
如图,已知点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=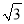 ,则?ABCD面积的最大值为_____.
,则?ABCD面积的最大值为_____.
查看答案和解析>>
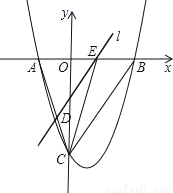
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:解答题
如图,抛物线y=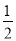 x2﹣
x2﹣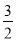 x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com