
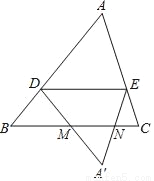
如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
(1)求证:DB=DM.
(2)若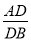 =2,DE=6,求线段MN的长.
=2,DE=6,求线段MN的长.
(3)若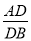 =n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
=n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(2) 题型:解答题
某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
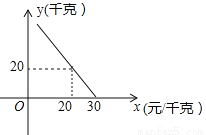
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
(1);(2)当销售单价为20元/千克时,每天可获得最大利润200元. 【解析】试题分析:(1)由图象过点(20,20)和(30,0),利用待定系数法求直线解析式; (2)每天利润=每千克的利润×销售量.据此列出表达式,运用函数性质解答. 试题解析:(1)设y=kx+b,由图象可知, , 解之,得: , ∴y=﹣2x+60; (2)p=(x﹣10)y ...查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:单选题
如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
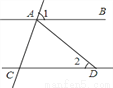
A. 80° B. 75° C. 70° D. 65°
C 【解析】∵AD=CD,∴∠DCA=∠DAC,∵∠2=40°,∴∠DCA=(180°-40°)÷2=70°,∵AB∥CD,∴∠1=∠DCA=70°.故选C.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
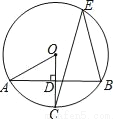
A. 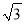 B. 4 C. 2
B. 4 C. 2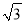 D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
环境监测中PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000001米,那么数据0.0000025用科学记数法可以表示为( )
A. 2.5×105 B. 2.5×106 C. 2.5×10﹣5 D. 2.5×10﹣6
D 【解析】由科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.因此0.0000025=2.5×10﹣6. 故选:D. 此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<1...查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
甲、乙两个袋中均有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为﹣7,﹣1,3,乙袋中的三张卡片上所标的数值分别为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上标的数值,把x、y分别作为点A的横坐标、纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况;
(2)求点A落在第二象限的概率.
(1)9(2) 【解析】试题分析:(1)直接利用表格列举即可解答; (2)利用(1)中的表格求出点A落在第三象限共有两种情况,再除以点A的所有情况即可. 【解析】 (1)如下表, ﹣7 ﹣1 3 ﹣2 (﹣7,﹣2) (﹣1,﹣2) (3,﹣2) 1 (﹣7,1) (﹣1,1) (3,1) 6 (﹣7,6) (﹣1,6) (3,6) 点A(x,y)...查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:填空题
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
解方程:
(1)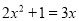 (配方法)
(配方法)
(2)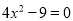 (因式分解法)
(因式分解法)
(3)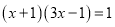 ( 公式法)
( 公式法)
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:解答题
在平面直角坐标系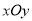 中,抛物线
中,抛物线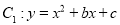 经过点
经过点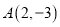 ,且与
,且与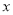 轴的一个交点为
轴的一个交点为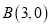 .
.
(1)求抛物线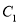 的表达式;
的表达式;
(2)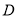 是抛物线
是抛物线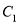 与
与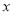 轴的另一个交点,点
轴的另一个交点,点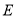 的坐标为
的坐标为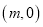 ,其中
,其中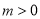 ,△
,△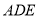 的面积为
的面积为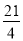 .
.
①求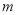 的值;
的值;
②将抛物线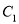 向上平移
向上平移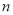 个单位,得到抛物线
个单位,得到抛物线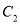 .若当
.若当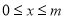 时,抛物线
时,抛物线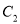 与
与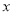 轴只有一个公共点,结合函数的图象,求
轴只有一个公共点,结合函数的图象,求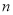 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com