
将一副三角板按如图所示放置摆放,已知∠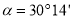 ,则∠
,则∠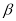 的度数是________.
的度数是________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:填空题
在数轴上,表示+4的点在原点的____侧,距原点____个单位.
右 4 【解析】由正数在原点右侧,负数在原点左侧,两数到原点的距离即是它们的绝对值,所以在数轴上,表示+4的点在原点的右侧,距原点4个单位. 故答案为:右,4.查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:解答题
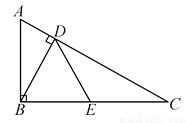
如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D ,点E为线段BC的中点,AD=2,tan A=2.
(1)求AB的长;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
顺次连结矩形各边中点所得的四边形是( ).
A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
B. 【解析】 试题分析:作出图形,根据三角形的中位线定理可得EF=GH=AC,FG=EH=BD,再根据矩形的对角线相等可得AC=BD,从而得到四边形EFGH的四条边都相等,然后根据四条边都相等的四边形是菱形解答. 如图,连接AC、BD ∵E、F、G、H分别是矩形ABCD的AB、BC、CD、AD边上的中点, ∴EF=GH=AC,FG=EH=BD, ∵矩形ABCD...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
已知: 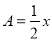 ,
, 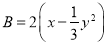 ,
, 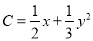 .
.
(1)试求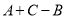 所得的结果;(用含
所得的结果;(用含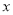 ,
, 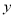 的式子表示)
的式子表示)
(2)若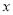 ,
, 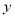 满足
满足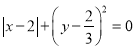 ,求(1)中所得结果的值.
,求(1)中所得结果的值.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
把一根长为120cm的木棍锯成两段,若使其中一段的长比另一段的2倍少3cm,则锯出的木棍的长不可能为( )
A. 80cm B. 41cm C. 79cm D. 41cm或79cm
C 【解析】试题解析:设一段为x,则另一段为(2x-3), 由题意得,x+2x-3=120, 解得:x=41(cm), 则另一段为:79(cm). 故选C.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
若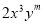 与
与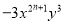 是同类项,则
是同类项,则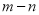 的值是( )
的值是( )
A. 3 B. 2 C. 1 D. 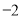
查看答案和解析>>
科目:初中数学 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:填空题
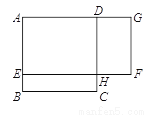
在北京市治理违建的过程中,某小区拆除了自建房,改建绿地. 如图,自建房占地是边长为8m的正方形ABCD,改建的绿地是矩形AEFG,其中点E在AB上,点G在AD的延长线上,且DG = 2BE. 如果设BE的长为x(单位:m),绿地AEFG的面积为y(单位:m2),那么y与x的函数的表达式为__________________;当BE =______m时,绿地AEFG的面积最大.
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上学期期末考试数学试卷 题型:解答题
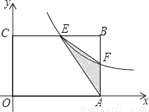
如图,在矩形OABC中,OA=6,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数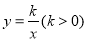 的图象与BC边交于点E.
的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com