
(1)计算:|﹣2|+(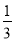 )﹣1﹣(
)﹣1﹣(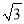 ﹣2010)0﹣
﹣2010)0﹣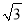 •tan60°
•tan60°
(2)先化简先化简,再求值: 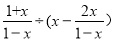 ,其中x=
,其中x=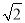 .
.
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源:2017年海南省文昌市中考数学模拟试卷 题型:填空题
已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为_____.
8或2 【解析】作AD⊥BC ,则AD即为BC边上的高. 【解析】 设圆心到的距离为,则依据垂径定理得. 当圆心在三角形内部时, 边上的高为; 当圆心在三角形外部时, 边上的高为 . “点睛”本题综合考查了垂径定理和勾股定理在圆中的应用,因三角形与圆心的位置不明确,注意分情况讨论.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.
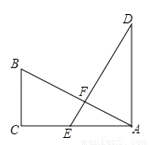
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
正方形是轴对称图形,它共有_______条对称轴.
四 【解析】试题分析:根据对称轴的定义,直接作出图形的对称轴即可. 【解析】 ∵如图所示,正方形是轴对称图形,它共有4条对称轴. 故答案为:4.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
以下各组数为边长的三角形中,能组成直角三角形的是( )
A. 1,2,3 B. 2,3,4 C. 3,4,5 D. 4,5,6
C 【解析】根据勾股定理的逆定理,可知, , , ,故只有3、4、5符合,可以构成直角三角形. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学模拟试卷 题型:填空题
如图是小明家今年1月份至5月份的每月用电量的统计图,据此推断他家这五个月的月平均用电量是_____度.
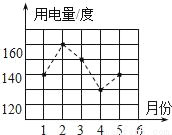
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学模拟试卷 题型:单选题
甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
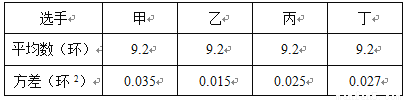
则这四人中成绩发挥最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
B 【解析】试题分析:根据方差的定义,方差越小数据越稳定. 试题解析:因为S甲2>S丁2>S丙2>S乙2,方差最小的为乙,所以本题中成绩比较稳定的是乙. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:填空题
已知点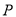 的坐标为
的坐标为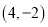 ,则点
,则点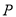 到
到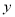 轴的距离为__________.
轴的距离为__________.
查看答案和解析>>
科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
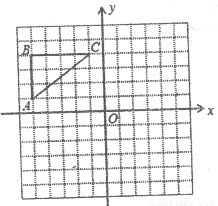
如图,在正方形网络中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
画出△ABC关于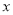 轴对称的△A1B1C1;
轴对称的△A1B1C1;
画出△ABC关于原点O对称的△A2B2C2;
点C1的坐标是 ;点C2的坐标是 ;
试判断:△A1B1C1与△A2B2C2是否关于y轴对称?(只需写出判断结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com