
以下各组数为边长的三角形中,能组成直角三角形的是( )
A. 1,2,3 B. 2,3,4 C. 3,4,5 D. 4,5,6
C 【解析】根据勾股定理的逆定理,可知, , , ,故只有3、4、5符合,可以构成直角三角形. 故选:C. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017年海南省文昌市中考数学模拟试卷 题型:解答题
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
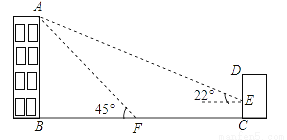
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈ ,cos22°≈
,cos22°≈ ,tan22°≈
,tan22°≈ )
)
查看答案和解析>>
科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:单选题
下面每组数分别是三根小木棒的长度, 它们能摆成三角形的是( )
A.5, 1, 3 B.2, 4, 2 C.3, 3, 7 D.2, 3, 4
D 【解析】A、3+1<5,不能构成三角形,故本选项错误; B、2+2=4,不能构成三角形,故本选项错误; C、3+3<7,不能构成三角形,故本选项错误; D、2+3>4,能构成三角形,故本选项正确, 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
如图,在△ABC中,DE是AC的垂直平分线,AE=5 cm,△ABC的周长为26cm,则△ABD的周长为_________cm.
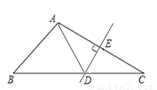
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A. 三边中线的交点 B. 三条角平分线的交点
C. 三边垂直平分线的交点 D. 三边上高的交点
C 【解析】试题分析:为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.∵三角形的三条垂直平分线的交点到中间的凳子的距离相等, ∴凳子应放在△ABC的三条垂直平分线的交点最适当. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学模拟试卷 题型:解答题
(1)计算:|﹣2|+(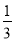 )﹣1﹣(
)﹣1﹣(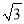 ﹣2010)0﹣
﹣2010)0﹣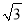 •tan60°
•tan60°
(2)先化简先化简,再求值: 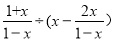 ,其中x=
,其中x=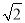 .
.
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学模拟试卷 题型:单选题
某校四个绿化小组某天的植树棵树如下:10,10,x,8.若这组数据的众数与平均数相等,那么这组数据的中位数是( )
A. 9 B. 10 C. 11 D. 12
B 【解析】试题解析:当x=8时,有两个众数,而平均数只有一个,不合题意舍去. 当众数为10,根据题意得 解得x=12, 将这组数据从小到大的顺序排列8,10,10,12, 处于中间位置的是10,10, 所以这组数据的中位数是(10+10)÷2=10. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:填空题
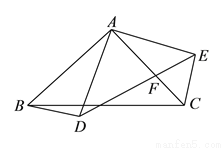
如图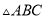 与
与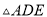 都是以
都是以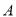 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, 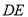 交
交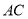 于点
于点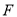 ,若
,若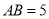 ,
, 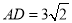 ,当
,当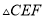 是直角三角形时,则
是直角三角形时,则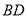 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
如图1,抛物线y= 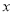 2+b
2+b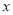 +c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)若M是抛物线的对称轴与直线BC的交点,N是抛物线的顶点,求MN的长;
(3)设点P是(1)中的抛物线的一个动点,是否存在满足S△PAB=8的点P?如存在请求出P的坐标;若不存在,请说明理由.
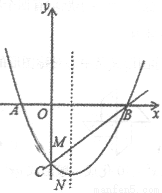
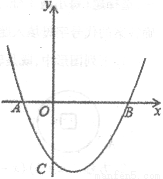
图1 备用图
(1)y=x2﹣2x﹣3;(2)1;(3)当P点的坐标分别为(1+2,4)、(1﹣2,4)、(1,﹣4)时,S△PAB=8. 【解析】试题分析:(1)把点A、B的坐标分别代入函数解析式,列出关于系数b、c的方程组,通过解方程组求得它们的值即可; (2)结合抛物线的解析式得到点C、N的坐标,利用B、C的坐标可以求得直线BC的解析式,由一次函数图象上点的坐标特征和点的坐标与图形的性质进行解...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com