练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知一次函数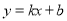的图象经过点（-2，-4），且与正比例函数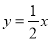的图象相交于点（4，a），求：

    （1）a的值；

    （2）k、b的值；

    （3）求出这两个函数的图象与y轴相交得到的三角形的面积．

    （1）2；（2）k=1，b=-2；（3）4 【解析】试题分析：（1）将点（4，a）代入即可求出a的值；（2）将（-2,-4）和点（4，a）代入一次函数解析式求解；（3）求出两个函数与y轴交点坐标，再根据三角形面积公式求解. 解：（1）将点（4，a）代入得a=×4=2； （2）将（-2,-4）和点（4，2）代入y=kx+b，得解得 （3）一次函数y=x-2与y轴交于点（0，-...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年河北省沧州市中考数学模拟试卷（六） 题型：填空题

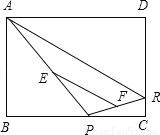
    如图，已知矩形ABCD，P、R分别是BC和DC上的点，E、F分别是PA，PR的中点．如果DR=3，AD=4，则EF的长为_____．

    2.5 【解析】试题分析：根据勾股定理求AR；再运用中位线定理求EF． 试题解析：∵四边形ABCD是矩形， ∴△ADR是直角三角形 ∵DR=3，AD=4 ∴AR= ∵E、F分别是PA，PR的中点 ∴EF=AR=×5=2．5．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级12月月考数学试卷 题型：解答题

    解方程：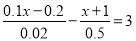

    x=5 【解析】试题分析：先去分母，在移项，合并同类项，系数化为1即可． 试题解析：5x-10-2x-2=3 3x=15 解得：x=5

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级12月月考数学试卷 题型：单选题

    如图所示，将一块直角三角板的直角顶点O放在直尺的一边CD上，如果∠AOC＝28°，那么∠BOD等于（ ）

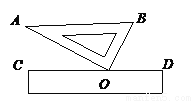
    A. 72° B. 62° C. 52° D. 28°

    B 【解析】∵∠AOC+∠BOD=90°, ∴∠BOD=90°-28°=62°. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：江苏省高邮市2017-2018学年八年级12月月考数学试卷 题型：解答题

    在平面直角坐标系中，若点P的坐标为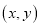,则定义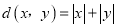： 为点P到坐标原点O的“折线距离”.

    （1）若已知P（-2，3），则点P到坐标原点O的“折线距离”d（-2，3）= ；

    （2）若点P（x，y）满足2x+y=0,且点P到坐标原点O的“折线距离”d（x，y）=6，求出P的坐标；

    （3）若点P到坐标原点O的“折线距离”d（x，y）=3，试在坐标系内画出所有满足条件的点P构成的图形，并求出该图形的所围成封闭区域的面积.

    （1）5；（2）（2，-4），（-2,4），（6，-12）或（-6,12）；（3）画图见解析，面积为18. 【解析】试题分析：（1）根据定义求出即可；（2）由d（x，y）==6，再由2x+y=0两式求出x、y；（3）由d（x，y）==3，得出①y=-x+3；②y=x-3；③y=x+3；④y=-x-3.分别画出四条直线，再求围成面积. 解：（1）d（-2，3）==5； （2）由d（...

    查看答案和解析>>

    科目：初中数学 来源：江苏省高邮市2017-2018学年八年级12月月考数学试卷 题型：填空题

    如图，一束光线从点O射出，照在经过A（2,0），B（0,2）的镜面上的点D，经AB反射后，反射光线又照到竖立在y轴位置的镜面，经y轴，再反射的光线恰好通过点A，则点D的坐标为__________．

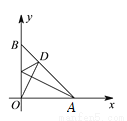
    （） 【解析】∵点O关于AB的对称点是O′（2，2）， 点A关于y轴的对称点是A′（-2，0）， 设直线AB的解析式为y=kx+b， ∵（2，0），（0，2）在直线AB上， ∴解得k=-1，b=2， ∴直线AB的解析式是y=-x+2， 同理可得O′A′的解析式是y=+1， 两式联立，得 解得x=,y=. 故答案为（）.

    查看答案和解析>>

    科目：初中数学 来源：江苏省高邮市2017-2018学年八年级12月月考数学试卷 题型：填空题

    若正数a的两个平方根分别为x和2x－6，则a＝_____________．

    4 【解析】根据平方根的定义，得x+2x-6=0，解得x=2， 则正数a为22=4. 故答案为4.

    查看答案和解析>>

    科目：初中数学 来源：浙江省杭州市西湖区绿城育华2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

    解不等式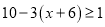，并在数轴上表示不等式的解集．

    【解析】试题分析：先去括号，再移项，合并同类项，把x的系数化为1，再把不等式的解集在数轴上表示出来即可． 试题解析：去括号得， ， 移项得， ， 合并同类项得， ， 系数化为得， ． 在数轴上表示为：

    查看答案和解析>>

    科目：初中数学 来源：河南省邓州市2018届九年级上学期期中质量评估---数学试卷word版 题型：解答题

    如图，在△ABC中，已知AB=AC=6，BC=9，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．

    （1）求证：△ABE∽△ECM；

    （2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；

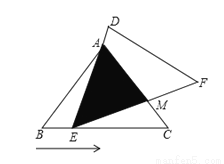
    （1）答案见解析；（2）3或5． 【解析】试题分析：（1）根据全等三角形的性质得到∠AEF=∠B，根据三角形的外角的性质得到∠CEP=∠BAE，根据相似三角形的判定定理证明即可； （2）由∠AEF=∠B=∠C，且∠AME＞∠C，得到∠AME＞∠AEF，从而AE≠AM；然后 分两种情况讨论：①当AE=EM时；②当AM=EM时． 试题解析：【解析】 （1）∵AB=AC，∴∠B...

    查看答案和解析>>

    同步练习册答案