
图中有五个半圆,四个小圆的直径刚好在大圆的直径上,且直径之和等于大圆直径,两只小虫同时从点A出发,以相同的速度爬向点B,甲虫沿大圆圆周运动,乙虫沿其余四个小圆的圆弧的路线爬行,则下列结论正确的是( )
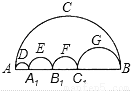
A. 甲先到点B B. 乙先到点B C. 甲、乙同时到达点B D. 无法确定
C 【解析】本题考查的是半圆的弧长 乙虫走的路线应该是4段半圆的长,那么应该是π(AA1+A1B1+B1C1+C1B)=π×AB,因此乙虫走的四段半圆的弧长正好和甲虫走的大半圆的弧长相等,因此两个同时到B点. 由图可知,π(AA1+A1B1+B1C1+C1B)=π×AB, 因此乙虫走的四段半圆的弧长正好和甲虫走的大半圆的弧长相等, 因此两个同时到B点. 故选C....科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:单选题
下列长度的三条线段能组成直角三角形的是( )
A. 4,5,6 B. 2,3,4 C. 1,1, 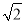 D. 1,2,2
D. 1,2,2
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
2014年3月14日,“玉兔号”月球车成功在距地球约384400公里远的月球上自主唤醒,将384400这个数用科学记数法表示为_____.
3.844×105 【解析】384400=3.844×105.查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年七年级(上)期末复习数学试卷 题型:解答题
分别画出下列平面图形:长方形,正方形,三角形,圆.
答案见解析. 【解析】本题考查的是平面图形的认识 长方形的主要特征:对边相等,四个角都是直角; 正方形的主要特征:四条边相等,四个角都是直角; 三条线段首尾顺次连接组成的平面图形叫做三角形; 利用刻度尺、直角三角板、圆规即可根据如上特征作出图形。查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年七年级(上)期末复习数学试卷 题型:填空题
若(a﹣2)2+|b+3|=0,则(a+b)2014=________.
1 【解析】试题解析: ∴a=2,b=?3, 故答案为:1.查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年七年级(上)期末复习数学试卷 题型:单选题
当1-(3m-5)2取得最大值时,关于x的方程5m-4=3x+2的解是( )
A. 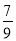 B.
B. 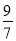 C. -
C. -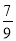 D. -
D. -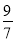
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:解答题
关于的一元二次方程x2+2x+k+1=0的有两个实数解是x1和x2.
(1)求k的取值范围;
(2)如果x1+x2-x1x2<-1且k为整数,求k的值.
(1)k≤0;(2)k的值为-1和0. 【解析】试题分析:(1)∵方程有实数根 ∴⊿=22-4k+1)≥0解得 k≤0. (2)根据一元二次方程根与系数的关系,得x1+x2=-2, x1x2=k+1 得 -2—( k+1)<-1 解得 k>-2 ∴ -2<k≤0 ∵k为整数 ∴k的值为-1和0. 试题解析:【解析】 ∵(1)方程有实数根 ∴⊿=22-4k+1)≥0....查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:单选题
使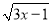 有意义的x的取值范围是( )
有意义的x的取值范围是( )
A. x>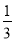 B. x>-
B. x>-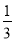 C. x≥
C. x≥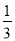 D. x≥-
D. x≥-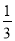
查看答案和解析>>
科目:初中数学 来源:2017年天津109中中考数学模拟试卷 题型:填空题
如图在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB,CA′相交于点D,则线段BD的长为___________.
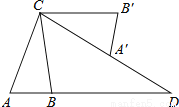
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com