
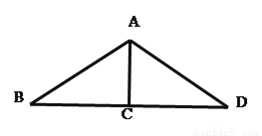
如图,在?ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.
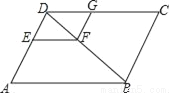
【答案】6
【解析】试题分析:根据平行线分线段成比例定理求出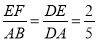 , 得到AB的长,根据平行四边形的性质求出CD,根据平行线分线段成比例定理得到比例式,计算即可.
, 得到AB的长,根据平行四边形的性质求出CD,根据平行线分线段成比例定理得到比例式,计算即可.
试题解析:∵EF∥AB,
∴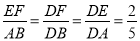 ,又EF=4,
,又EF=4,
∴AB=10,
∵四边形ABCD是平行四边形,
∴CD=AB=10,
∵FG∥ED,
∴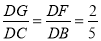 ,
,
∴DG=4,
∴CG=6.
【题型】解答题
【结束】
22
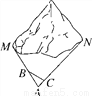
如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:填空题
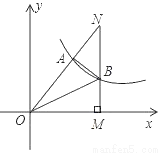
如图,双曲线y=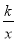 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为6,则k的值是_____.
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为6,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如果一个三角形的三个内角都相等,那么这个三角形的形状是________.
等边三角形 【解析】【解析】 ∵一个三角形的三个内角都相等,∴每个角等于60°,∴这个三角形的形状是等边三角形.故答案为:等边三角形.查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
下列计算正确的是( )
A. a3+a2=a5 B. a3•a2=a5 C. (a3)2=a9 D. a3﹣a2=a
B 【解析】试题解析:A. a3+a2≠a5,故原选项错误; B. a3•a2=a5,正确; C. (a3)2=a6,故原选项错误; D. a3﹣a2≠a,故原选项错误. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
在等腰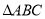 中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即
中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即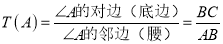 .例:T(60
.例:T(60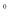 )=1,那么T(120
)=1,那么T(120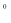 )=____________ ;
)=____________ ;
【答案】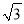
【解析】作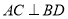 ,垂足为C.
,垂足为C.
设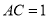
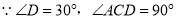
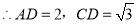
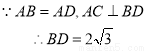
则T(120 )=
)=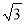
【题型】填空题
【结束】
17
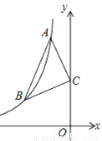
如图:已知点A、B是反比例函数y=﹣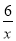 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:单选题
如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
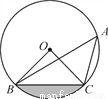
A. π-4 B.  π-1 C. π-2 D.
π-1 C. π-2 D.  -2
-2
【答案】C
【解析】试题解析:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴△OBC的BC边上的高为: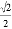 OB=
OB=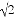 ,
,
∴BC=2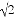
∴S阴影=S扇形OBC﹣S△OBC=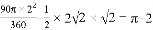 .
.
故选C.
【题型】单选题
【结束】
10
夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )
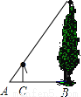
A.8m B.6.4m C.4.8m D.10m
A. 【解析】 试题分析:因为人和树均垂直于地面,所以和光线构成的两个直角三角形相似, 设树高x米,则,即,解得,x=8. 故选A.查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:解答题
计算:﹣12016﹣[2﹣(﹣1)2016]÷(﹣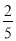 )×
)×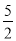 .
.
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上期末模拟数学试卷 题型:单选题
某中学九(1)班学生为希望工程捐款,该班50名学生的捐款情况统计如图,则他们捐款金额的众数和中位数分别是( )
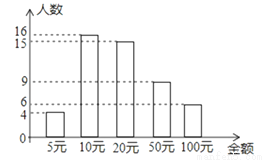
A. 16,15 B. 15,16 C. 20,10 D. 10,20
D 【解析】∵10出现了16次,出现的次数最多, ∴他们捐款金额的众数是10; ∵共有50个数, ∴中位数是第25、26个数的平均数, ∴中位数是(20+20)÷2=20; 故选:D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com