
��ͼ��˫����y=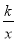 ����Rt��OMNб���ϵĵ�A����ֱ�DZ�MN�ཻ�ڵ�B����֪OA=2AN����OAB�����Ϊ6����k��ֵ��_____��
����Rt��OMNб���ϵĵ�A����ֱ�DZ�MN�ཻ�ڵ�B����֪OA=2AN����OAB�����Ϊ6����k��ֵ��_____��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�Ϸ���2016-17ѧ��ȵ�һѧ����ĩ��ѧ����������꼶��ѧ�Ծ� ���ͣ������
����˵���У�
����a+b+c=0���� (a+c)2=b2.
����a+b+c=0����x=1һ���ǹ���x�ķ���ax+b+c=0�Ľ�.
����a+b+c=0����abc��0����abc��0.
����a+b+c=0���� | a |=| b+c |.
������ȷ����____________.
�٢ڢ�. ������������a+c=?b����ƽ��,��(a+c)2=b2������ȷ�� �ڽ�x=1�������x�ķ���ax+b+c=0(a��0)�����̳���������ȷ�� ����a+b+c=0��abc��0���ɵ�a��b��c����һ������������������һ���������������������abc>0��abc<0���ʴ��� ����a=?(c+b)�ɵã�|a|=|b+c|������ȷ. �ʴ�Ϊ���٢ڢ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������2018����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
��ͼ�����������ι��ţ���������ˮ��2��ʱ��ˮ���4�ף���ˮ���½�1�ף���ˮ����Ƚ����Ӷ����ף�
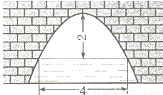
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������2018����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ���ѡ��
��ͼ��һ����ֽ����ȫ�����������AB��AC�ļн�Ϊ120�㣬AB��Ϊ25cm����ֽ���ֵĿ�BDΪ15cm����ֽ��������ֽ������ֽ�����Ϊ�� ��

A. 175��cm2 B. 350��cm2 C. 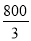 ��cm2 D. 150��cm2
��cm2 D. 150��cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ������� ���ͣ������
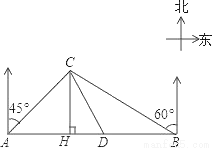
ij���ԭ����һ����ֱ�Ĺ�·���ڽ�����·���40ǧ��A��B���أ��ֱ��мס�������ҽ��վ����ͼ����A�ر�ƫ��45�㣬B�ر�ƫ��60�㷽������һ������C������C��CH��AB��H��
��1����������C��B�صľ��루����ø�ʽ��ʾ����
��2��һ�죬��ҽ�ƶӵ�ҽ��Ҫ��������C���������B�ش�ع�·AB��D����BD��AB��ת��������D����DC����������C����C��D���ؾ�����B��C���ؾ����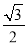 ������B��D���صľ��룮�������ȷ��0.1ǧ�� �ο����ݣ�
������B��D���صľ��룮�������ȷ��0.1ǧ�� �ο����ݣ� 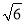 ��2.449��
��2.449�� 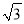 ��1.732��
��1.732�� 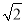 ��1.414��
��1.414��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ������� ���ͣ������
�ҹ������㵺����Χ�������Լ170000km2�������ÿ�ѧ�������ɱ�ʾΪ_____��
1.7��105 ��������������������ݿ�ѧ�������ĸ����֪���ÿ�ѧ�������ɽ�һ������ʾ����ʽ�������ÿ�ѧ��������ʾ170000km2=km2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ������� ���ͣ���ѡ��
����ͼ���У�����Գ�ͼ�ε��ǣ�������
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
��ͼ����һ�����ǰ尴ͼ�з�ʽ���ţ���Ǧ����ڣ� ��
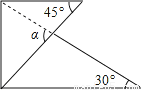
A. 30�� B. 45�� C. 60�� D. 75��
D ������������������ȸ���ֱ�����ǰ�������������ACD�Ķ������ٸ��ݡϦ��ǡ�ACE����ǽ��н�� �������� ��ͼ����һ�����ǰ���ţ� ���ACB=90�㣬��BCD=45�㣬 ���ACD=��ACB����BCD=90�㩁45��=45�㣬 �ߡϦ��ǡ�ACE����ǣ� ��Ϧ�=��A+��ACD=30��+45��=75�㣮 ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ����2018����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
��ͼ����?ABCD�У�EF��AB��FG��ED��DE��DA=2��5��EF=4�����߶�CG�ij���
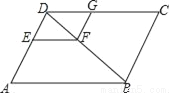
���𰸡�6
���������������������ƽ���߷��߶γɱ����������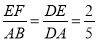 �� �õ�AB�ij�������ƽ���ı��ε��������CD������ƽ���߷��߶γɱ��������õ�����ʽ�����㼴�ɣ�
�� �õ�AB�ij�������ƽ���ı��ε��������CD������ƽ���߷��߶γɱ��������õ�����ʽ�����㼴�ɣ�
�����������EF��AB��
��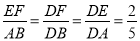 ����EF=4��
����EF=4��
��AB=10��
���ı���ABCD��ƽ���ı��Σ�
��CD=AB=10��
��FG��ED��
��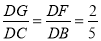 ��
��
��DG=4��
��CG=6��
�����͡������
��������
22
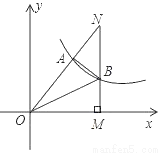
��ͼ��M��NΪɽ�����������ׯ��Ϊ�����彻ͨ���㣬���ݹ��ҵĻ������ߣ�����������һֱ�ߺ�����������ԱΪ���㹤�������������M��N����֮���ֱ�߾��룮ѡ�������A��B��C����B��C�ֱ���AM��AN�ϣ��ֲ��AM��1ǧ�ף�AN��1.8ǧ�ף�AB��54�ף�BC��45�ף�AC��30�ף���M��N����֮���ֱ�߾��룮
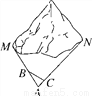
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com