练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

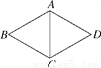
    如图，已知菱形ABCD的边长为3，∠ABC=60°，则对角线AC的长是（ ）

    A. 12 B. 9 C. 6 D. 3

    D 【解析】 ∵四边形ABCD是菱形， ∴AB=BC， ∴△ABC是等腰三角形， ∵∠ABC=60°， ∴△ABC是等边三角形， ∴AB=BC=AC， ∵菱形ABCD的边长为3， ∴AB=BC=3， ∴AC=3. 故本题应选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：单选题

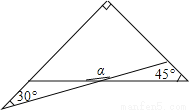
    一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（　　）

    A. 165° B. 120° C. 150° D. 135°

    A 【解析】利用直角三角形的性质求得∠2=60°；则由三角形外角的性质知∠2=∠1+45°=60°，所以易求∠1=15°；然后由邻补角的性质来求∠α的度数． 【解析】 如图， ∵∠2=90°-30°=60°，∴∠1=∠2-45°=15°，∴∠α=180°-∠1=165°．故选A．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：单选题

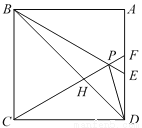
    如图，在正方形ABCD中，△BPC是等边三角形，BP，CP的延长线分别交AD于点E，F，连接BD，DP，BD与CF交于点H．下列结论：①BE=2AE；②△DFP∽△BPH；③△PFD∽△PDB；④DP2=PH•PC，其中正确的结论是

    A. ①②③④ B. ②③ C. ①②④ D. ①③④

    C 【解析】试题分析：∵△BPC是等边三角形， ∴BP=PC=BC，∠PBC=∠PCB=∠BPC=60°， 在正方形ABCD中， ∵AB=BC=CD，∠A=∠ADC=∠BCD=90° ∴∠ABE=∠DCF=30°， ∴BE=2AE；故①正确； ∵PC=CD，∠PCD=30°， ∴∠PDC=75°， ∴∠FDP=15°， ∵∠DBA=45°...

    查看答案和解析>>

    科目：初中数学 来源：安徽省宿州市（城西校区） 2017-2018学年九年级第一学期期中测试数学试卷 题型：填空题

    若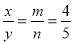 (y≠n)，则＝____．

    【解析】∵（y≠n）， ∴ ， ∴＝ ， 故答案为： .

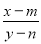    查看答案和解析>>

    科目：初中数学 来源：安徽省宿州市（城西校区） 2017-2018学年九年级第一学期期中测试数学试卷 题型：单选题

    若一元二次方程x2－2x－m＝0无实数根，则一次函数y＝(m＋1)x＋m－1的图象不经过第(　　)象限．

    A. 四 B. 三 C. 二 D. 一

    D 【解析】试题分析：∵一元二次方程x2 - 2x - m = 0无实数根 ∴△=4+4m<0,即m<-1 ∴一次函数的比例系数m+1<0,图像经过二四象限 截距m-1<0，则图象与y轴交与负半轴，图像过第三象限 ∴一次函数y =" (m+1)x" + m - 1的图像不经过第一象限，故选D

    查看答案和解析>>

    科目：初中数学 来源：2017年安徽省中考数学三模试卷 题型：解答题

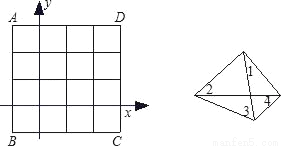
    如图，放在平面直角坐标系中的正方形ABCD的边长为4，现做如下实验：抛掷一枚均匀的正四面体骰子（如图，它有四个顶点，各顶点数分别是1、2、3、4），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的点数作为直角坐标系中点P的坐标（第一次的点数为横坐标，第二次的点数为纵坐标）．

    （1）求点P落在正方形面上（含边界，下同）的概率；

    （2）将正方形ABCD平移数个单位，是否存在一种平移，使点P落在正方形面上的概率为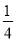？若存在，指出其中的一种平移方式；若不存在，说明理由．

    （1）；（2）． 【解析】【试题分析】 （1）列表格把每种情况都列举出来，看看满足条件的有几种，然后作比即可. （2）将正方形向左平移1个单位，向下平移1个单位就能够满足条件. 【试题解析】 （1）由图可知，点P落在正方形面上（含边界，下同）的情况是：（1，1），（2，1），（3，1），（1，2），（2，2），（3，2），（1，3），（2，3），（3，3）；概率是：9...

    查看答案和解析>>

    科目：初中数学 来源：2017年安徽省中考数学三模试卷 题型：填空题

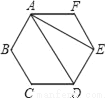
    如图，AD、AE是正六边形的两条对角线，不添加任何辅助线，请写出两个正确的结论：

    （1）_____；

    （2）_____．（只写出两个你认为正确的结论即可）．

    三角形AFE是等腰三角形 四边形ABCD是等腰梯形 【解析】示例三角形AFE是等腰三角形；四边形ABCD是等腰梯形．答案不唯一．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 期末测评 题型：解答题

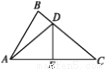
    如图，已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.

    (1)求∠BAD的度数；

    (2)若AB=10,BC=12,求△ABD的周长.

    （1）20°；（2）22. 【解析】试题分析：（1）根据三角形内角和定理求出∠C，根据线段垂直平分线的性质得到DA=DC，求出∠DAC，计算即可； （2）根据DA=DC，三角形的周长公式计算． 【解析】 (1)∵∠BAC=60°,∠B=80°, ∴∠C=180°-∠BAC-∠B=180°-60°-80°=40°, ∵DE垂直平分AC,∴DA=DC. ∴∠DAC...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末考试数学试卷 题型：单选题

    在平面直角坐标系中，点P（2，一 4）关于原点对称的点的坐标是（ ）

    A. （2,4 ） B. （一2，4） C. （一2，一4） D. （一4，2）

    B 【解析】【解析】 点P（2，一 4）关于原点对称的点的坐标是（－2，4）．故选B．

    查看答案和解析>>

    同步练习册答案