
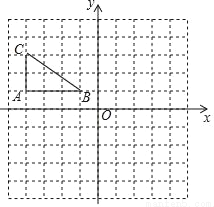
��ͼ����ֱ������ϵxOy�У���ABC��������������ֱ�ΪA����4��1����B����1��1����C����4��3����
��1������Rt��ABC����ԭ��O�����ĶԳƵ�ͼ��Rt��A1B1C1��
��2����Rt��ABC��Rt��A2BC2���ڵ�B���ĶԳƣ����A2������Ϊ�� ����C2������Ϊ�� ����
��3�����A�Ƶ�B��ת180�㵽��A2ʱ����A���˶������о�����·�̣�
 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������Դ��2016-2017ѧ���һѧ����ĩ���Ծ��꼶��ѧ�Ծ� ���ͣ������
�ⷽ�̣�x2��5 = 4x��
x1=5��x2=��1�� ��������������������������ʽ�ֽⷨ��ɣ� ����������������� ��x2��5=4x����x2��4x��5=0���ࣨx��5����x+1��=0����x��5=0����x+1=0����x1=5��x2=��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ����A��B��C�ǡ�O�ϵ����㣬����A =40º�����BOC�Ķ����ǣ�������
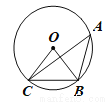
A. 100º B. 80º C. 60º D. 40º
B ���������ߡ�A =40º�� ���BOC=40º��2=80��. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ��PA��PB�ǡ�O���������ߣ��е�ֱ���A��B�����OP=4,PA=2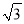 ����ô
����ô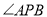 ����
����
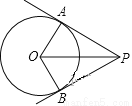
A. 90�� B. 100�� C. 60�� D. 110��
C ��������cos��APO==�����ԡ�APO=30��, .����ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹų������ţ����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
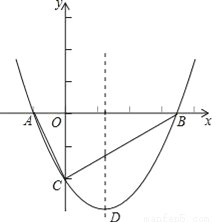
��ͼ��������y=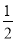 x2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��A����1��0����
x2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��A����1��0����
��1���������ߵĽ���ʽ������D�����ꣻ
��2���жϡ�ABC����״��֤����Ľ��ۣ�
��3����M��x���ϵ�һ�����㣬����DCM���ܳ���Сʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹų������ţ����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ��һ���뾶Ϊ2cm��Բ�̱��ָ��ʮ������. ���У���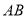 ��
��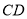 ����Բ��
����Բ��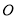 �Գƣ�
�Գƣ� 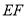 ��
��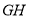 ����Բ��
����Բ��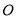 �Գƣ�������Ͷ��һ���壬������������Ӱ���ֵĸ���Ϊ_____________��
�Գƣ�������Ͷ��һ���壬������������Ӱ���ֵĸ���Ϊ_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹų������ţ����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ABC�����߳��ֱ�Ϊ6��8��10���������Բ�İ뾶�ǣ�������
A. 3 B. 4 C. 5 D. 10
C ���������������� �ߣ����ABC��ֱ�������Σ�б��=10�������Բ�뾶=��10=5����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����������ɽ��2018����꼶��ѧ�ڰ�У������ѧ�Ծ� ���ͣ������
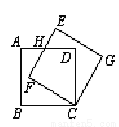
��ͼ���߳�Ϊ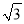 ��������ABCD�Ƶ�C��˳ʱ�뷽����ת30���õ���������EFCG��EF��AD�ڵ�H����ôAH�ij�Ϊ______.
��������ABCD�Ƶ�C��˳ʱ�뷽����ת30���õ���������EFCG��EF��AD�ڵ�H����ôAH�ij�Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ�Թ���2016��2017ѧ����ѧ�ڰ��꼶��ĩͳһ������ѧ�Ծ� ���ͣ������
��ϸ�Ķ����ϣ��ٳ��Խ�����⣺
��ȫƽ��ʽ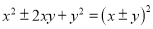 �Լ�
�Լ�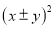 ��ֵΪ�Ǹ������ص�����ѧѧϰ���й㷺��Ӧ�ã�����̽��
��ֵΪ�Ǹ������ص�����ѧѧϰ���й㷺��Ӧ�ã�����̽��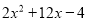 �����С��ֵʱ�����ǿ�������������
�����С��ֵʱ�����ǿ�������������
��������
ԭʽ = 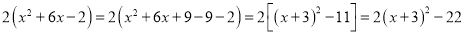 .
.
��Ϊ����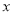 ȡʲô��������
ȡʲô��������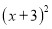 ��ֵΪ�Ǹ���������
��ֵΪ�Ǹ���������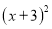 ����СֵΪ0����ʱ
����СֵΪ0����ʱ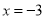 ʱ������
ʱ������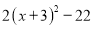 ����Сֵ��
����Сֵ��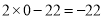 �����Ե�
�����Ե�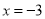 ʱ��ԭ����ʽ����Сֵ��
ʱ��ԭ����ʽ����Сֵ��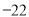 .
.
���������Ľ���˼·��̽��
��.����ʽ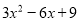 ����Сֵ�Ƕ��٣���д����Ӧ��
����Сֵ�Ƕ��٣���д����Ӧ��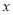 ��ȡֵ��
��ȡֵ��
��.����ʽ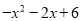 �����ֵ�Ƕ��٣���д����Ӧ��
�����ֵ�Ƕ��٣���д����Ӧ��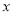 ��ȡֵ.
��ȡֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com