
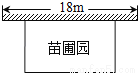
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
科目:初中数学 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
下列因式分解正确的是( ).
A. 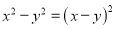 B.
B. 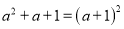 C.
C. 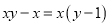 D.
D. 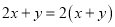
查看答案和解析>>
科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:解答题
一个多边形的内角和与某一个外角的度数总和为1350°,求这个多边形的边数.
九 【解析】试题分析:根据多边形的内角和公式可知180×7=1260<1350<180×8=1440,所以一个外角只能为1350﹣1260=90,由此得出多边形的边数为7+2=9求得问题. 试题解析:【解析】 设这个多边形的边数为n,180×(n﹣2)=1350﹣,180×7=1260<1350<180×8=1440,所以一个外角只能为1350﹣1260=90,由此得出多边形的边数为...查看答案和解析>>
科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:填空题
如果一个角的两边分别垂直于另一个角的两边,其中一个角为65°,则另一个角为___度.
65°或115° 【解析】【解析】 如图所示,设∠1=65°,则∠1和∠2,∠1和∠3两对角符合条件. 根据平行线的性质,得到∠1=∠2=65°. 结合邻补角的定义,得∠1+∠3=∠2+∠3=180°,得到∠3=115°. 故另一个角为65或115度.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:解答题
为解决消费者停车难的问题,某商场新建一小型轿车停车场,经测算,此停车场每天需固定支出的费用(包括设施维修费、管理人员工资等)为600元,为制定合理的收费标准,该商场对每天轿车停放辆次(每辆轿车每停放一次简称为“辆次”)与每辆轿车的收费情况进行调查,发现每辆次轿车的停车费定价不超过10元时,每天来此停放的轿车都为300辆次;若每辆次轿车的停车费定价超过10元,则每超过1元,每天来此停放的轿车就减少12辆次,设每辆次轿车的停车费x元(为便于结算,停车费x只取整数),此停车场的日净收入为y元(日净收入=每天共收停车费﹣每天固定的支出)回答下列问题:
(1)①当x≤10时,y与x的关系式为: ;
②当x>10时,y与x的关系式为: ;
(2)停车场能否实现3000元的日净收入?如能实现,求出每辆次轿车的停车费定价,如不能实现,请说明理由;
(3)该商场要求此停车场既要吸引顾客,使每天轿车停放的辆次较多,又要有最大的日净收入,按此要求,每辆次轿车的停车费定价应定为多少元?此时最大日净收入是多少元?
(1)①y=300x﹣600;②y=﹣12x2+420x﹣600;(2)停车场能实现3000元的日净收入,每辆次轿车的停车费定价是15元或20元;(3)每辆次轿车的停车费定价应定为17元,此时最大日净收入是3072元. 【解析】试题分析:(1)、①、当x≤10时,总费用=300×单价-工资得出答案;②、x>10时,停车的数量为:300-12(x-10),然后根据总费用=定价×数量-工资得出函...查看答案和解析>>
科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )
A.20 B.1508 C.1550 D.1558
D. 【解析】 试题分析:∵一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,且15≤x≤22, ∴当x=20时,y最大值=1558. 故选D.查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
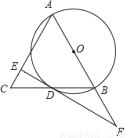
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
如图,△ABC中,P为AB上一点,在下列四个条件中,①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB,其中能满足△APC和△ACB相似的条件是( )
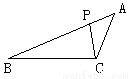
A、①②④ B、①③④ C、②③④ D、①②③
D 【解析】 试题分析:由图可得△APC和△ACB已经有一个公共角∠A,再根据相似三角形的判定方法依次分析各小题即可判断. ①∠ACP=∠B,②∠APC=∠ACB,③即,能满足; ④即,夹角应为∠B,故不能满足; 故选D.查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册 第23章 旋转 同步单元检测试卷(Word版附答案) 题型:解答题
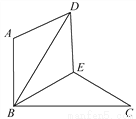
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com