
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:浙江省2017-2018学年八年级上学期第二次学情检测数学试卷 题型:解答题
某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
(1)30(5-x) 280(5-x);(2)4;(3)最省钱的租车方案是A型3辆,B型2辆. 【解析】试题分析: (1)由题意和表格中已有数据可知:B型车共计载客30(5-x)人,B型车共需租金280(5-x)元,把这两个式子填入相应表格即可; (2)把两种车各自所需租金相加,根据总费用不超过1900元列出不等式,解不等式求得最大整数解即可得到答案; (3)把两种车各自的...查看答案和解析>>
科目:初中数学 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:单选题
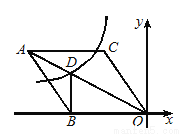
如图所示,在平面直角坐标系中,坐标原点O是菱形ABOC的一个顶点,边OB落在x轴的负半轴上,且cos∠BOC=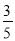 ,顶点C的坐标为(a,4),反比例函数
,顶点C的坐标为(a,4),反比例函数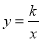 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A. 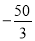 B.
B. 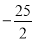 C.
C. 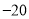 D.
D. 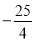
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年七年级上学期中考试数学试卷 题型:填空题
如图,在长方形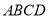 中,放入
中,放入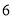 个形状和大小都相同的小长方形,已知小长方形的长为
个形状和大小都相同的小长方形,已知小长方形的长为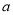 ,宽为
,宽为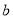 ,且
,且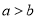 ,则长方形
,则长方形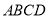 的周长为__________.(用含
的周长为__________.(用含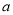 、
、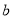 的代数式表示)
的代数式表示)

查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年七年级上学期中考试数学试卷 题型:填空题
在数轴上表示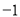 的点相距
的点相距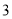 个单位长度的点表示的数是__________.
个单位长度的点表示的数是__________.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年七年级上学期中考试数学试卷 题型:单选题
李白出生于公元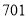 年,记作
年,记作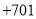 ,那么秦始皇出生于公元前
,那么秦始皇出生于公元前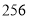 年,可记作( ).
年,可记作( ).
A. 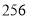 B.
B. 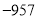 C.
C. 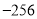 D.
D. 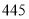
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:解答题
解下列方程:
(1)2﹣3(2﹣x)=4﹣x;
(2)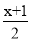 ﹣1=
﹣1=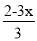 .
.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:单选题
若一个多项式减去a2﹣3b2等于a2+2b2,则这个多项式是( )
A. ﹣2a2+b2 B. 2a2﹣b2 C. a2﹣2b2 D. ﹣2a2﹣b2
B 【解析】结合整式加减法的运算法则进行求解即可. 【解析】 ∵一个多项式减去a2﹣3b2等于a2+2b2, ∴这个多项式为(a2﹣3b2)+(a2+2b2)= 2a2﹣b2. 故选B.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上学期第二次月考数学试卷 题型:填空题
抛物线y=﹣x2﹣2x+3与x轴交点为__________________,与y轴交点为______.
(﹣3,0)、(1,0) (0,3). 【解析】试题解析: ∵当时, , ∴与轴交点为 ∵当时, 解得: 或, ∴抛物线与轴交点为(?3,0)、(1,0); 故答案为(?3,0),(1,0);(0,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com