
同圆的内接正三角形与内接正方形的边长的比是( )
A. 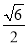 B.
B. 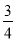 C.
C. 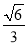 D.
D. 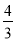
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:2x2+5x﹣3=0.(因式分解法)
x1=,x2=﹣3. 【解析】x2+5x﹣3=0, (2x﹣1)(x+3)=0, 2x﹣1=0或x+3=0, 所以x1=,x2=﹣3.查看答案和解析>>
科目:初中数学 来源:江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型:填空题
如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积和是49cm2,则其中最大的正方形S的边长为__________cm.
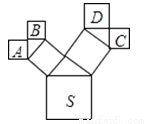
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
(1)70;(2). 【解析】试题分析:(1)由题意可得该顾客至多可得到购物券:50+20=70(元); (2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与该顾客所获得购物券的金额不低于50元的情况,再利用概率公式即可求得答案. 试题解析:(1)则该顾客至多可得到购物券:50+20=70(元); (2)画树状图得: ∵共有12种等可能的结果,该顾客所获得...查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:填空题
如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加_____条件,才能保证四边形EFGH是矩形.
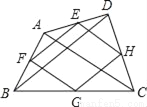
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:单选题
已知反比例函数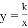 的图象过点P(1,3),则该反比例函数图象位于( )
的图象过点P(1,3),则该反比例函数图象位于( )
A. 第一、二象 B. 第一、三象限 C. 第二、四象限 D. 第三、四象限
B 【解析】试题解析:∵反比例函数y=的图象过点P(1,3), ∴k=1×3=3>0, ∴此函数的图象在一、三象限. 故选:B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
如图,直线y=﹣x+3与x轴,y轴分别相交于点B,C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)求该抛物线的函数表达式;
(2)请问在抛物线上是否存在点Q,使得以点B,C,Q为顶点的三角形为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由;
(3)过S(0,4)的动直线l交抛物线于M,N两点,试问抛物线上是否存在定点T,使得不过定点T的任意直线l都有∠MTN=90°?若存在,请求出点T的坐标;若不存在,请说明理由.
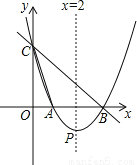
查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:填空题
将一元二次方程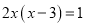 化成一般形式为 .
化成一般形式为 .
查看答案和解析>>
科目:初中数学 来源:安徽省亳州市利辛县2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知直线l与直线y=-2x平行,且经过点(-1,-2)求直线l与坐标轴围成的三角形的面积.
该函数图像与坐标轴围成的三角形的面积为4. 【解析】试题分析:根据直线l与直线y=-2x平行,可设直线l的解析式为y=-2x+b,根据直线l经过点(-1,-2),即可求得b值,再求得直线l与坐标轴的交点坐标,即可求得围成的三角形的面积. 试题解析: 设一次函数关系式为y=-2x+b, 将(-1,-2)代入上式得-2×(-1)+b=-2,解得b=-4, 即y=-2x-4...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com