
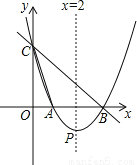
��ͼ��ֱ��y=��x+3��x�ᣬy��ֱ��ཻ�ڵ�B��C������B��C�����������y=ax2+bx+c��x�����һ����ΪA������ΪP���ҶԳ�����ֱ��x=2��
��1����������ߵĺ�������ʽ��
��2�����������������Ƿ���ڵ�Q��ʹ���Ե�B��C��QΪ�����������Ϊֱ�������Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
��3����S��0��4���Ķ�ֱ��l����������M��N���㣬�������������Ƿ���ڶ���T��ʹ�ò�������T������ֱ��l���С�MTN=90�㣿�����ڣ��������T�����ꣻ�������ڣ���˵�����ɣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������� 2017-2018ѧ�� ���꼶��ѧ�ϲ� һԪ���η��� ��ʽ�ֽⷨ ר����ϰ�����𰸣� ���ͣ������
����x2��9=0�Ľ���______��
x=��3�� ��������x2��9=0 (x-3)(x+3)=0 ����x1=3��x2=-3.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ������
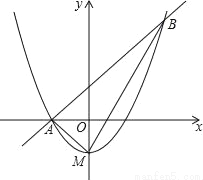
��ͼ������M��y���ϵ���������ֱ��y=x+1�ཻ��A��B���㣬�ҵ�A��x���ϣ���B�ĺ�����Ϊ2������AM��BM��
��1���������ߵĺ�����ϵʽ��
��2���жϡ�ABM����״����˵�����ɣ�
��3������������ֱ��y=x�Ľ����Ϊ�����ߵIJ����㣮������1����������ƽ�ƣ�ʹ�䶥��Ϊ��m��2m������m����ʲô����ʱ��ƽ�ƺ�����������в����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
ͬԲ���ڽ������������ڽ������εı߳��ı��ǣ�������
A. 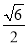 B.
B. 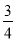 C.
C. 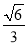 D.
D. 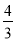
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ����DE��BC���ҡ�DCE=��B����ô����˵���У�������ǣ��� ����
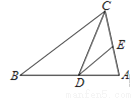
A. ��ADE�ס�ABC B. ��ADE�ס�ACD C. ��ADE�ס�DCB D. ��DEC�ס�CDB
C �������������������DE��BC�� ���ADE�ס�ABC����BCD=��CDE����ADE=��B����AED=��ACB�� �ߡ�DCE=��B�� ���ADE=��DCE�� �֡ߡ�A=��A�� ���ADE�ס�ACD�� �ߡ�BCD=��CDE����DCE=��B�� ���DEC�ס�CDB�� �ߡ�B=��ADE�� ���ǡ�BCD����AED���ҡ�BCD�١�A�� ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����ѧ�������г�����ѧ��ĩ�ۺϼ�� ���ͣ������
��ͼ��Ҫ��һ�����Ϊ45 m2�ij�����������(��Ϊ��Ƭ)����������һ�߿���һ�泤Ϊ14m��ǽ�������������ܳ�Ϊ22 m�������Χ�ɣ�ÿƬ��������ǰ�����һ����l m����.������������ij����.
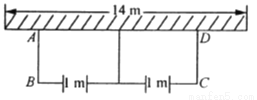
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����ѧ�������г�����ѧ��ĩ�ۺϼ�� ���ͣ������
��һԪ���η���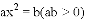 ���������ֱ���
���������ֱ���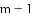
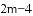
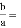 ________.
________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ij���ݷ��2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
���ʽ���̣�
��1��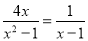
��2��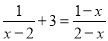 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������������2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ѧ��С������һ����ˮ�������ܽ��ӿ̻��Ɑˮ��ˮ��y(��)��ʱ��t(h)�ĺ�����ϵ��ͼ���ǣ� ��
A. 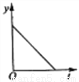 B.
B. 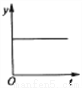 C.
C. 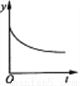 D.
D. 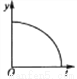
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com