
科目:初中数学 来源:山东省德州地区2017-2018学年度七年级第一学期期末检测数学试卷 题型:单选题
已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )

A. a•b>0 B. a+b<0 C. |a|<|b| D. a﹣b>0
D 【解析】试题分析:根据点a、b在数轴上的位置可知1<a<2,﹣1<b<0, ∴ab<0,a+b>0,|a|>|b|,a﹣b>0,. 故选:D.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十六章达标检测卷 题型:解答题
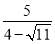 -
-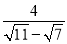 -
-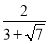 ;
;
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十六章达标检测卷 题型:填空题
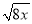 ,
, 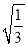 ,
, 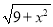 都不是最简二次根式.(____)
都不是最简二次根式.(____)
查看答案和解析>>
科目:初中数学 来源:2018届中考数学专题复习同步练习题:一次函数 题型:解答题
直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
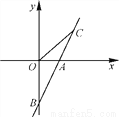
(2)若直线AB上一点C在第一象限且点C的坐标为(2,2),求△BOC的面积.
(1) y=2x-2(2)2 【解析】试题分析:(1)设直线AB的解析式为 将点点分别代入解析式即可组成方程组,从而得到AB的解析式; (2)以OB为底边,C到OB的垂线段为高,根据三角形的面积公式即可求解. 试题解析:(1)设直线AB的解析式为y=kx+b(k≠0), ∵直线AB过点A(1,0)、点B(0,?2), ∴ 解得 ∴直线AB的解析式为y=2x?2; ...查看答案和解析>>
科目:初中数学 来源:2018届中考数学专题复习同步练习题:一次函数 题型:单选题
要使直线y=(2m-3)x+(3n+1)的图象经过一、二、四象限,则m与n的取值为( )
A. m>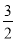 ,n>
,n>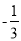 B. m>3,n>-3
B. m>3,n>-3
C. m<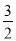 ,n<
,n<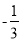 D. m<
D. m<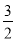 ,n>
,n>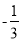
查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型:解答题
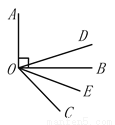
如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型:单选题
如图,两条直线相交于一点O,则图中共有( )对邻补角
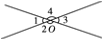
A. 2 B. 3 C. 4 D. 5
C 【解析】试题分析:图中的邻补角有:∠1和∠4,∠1和∠2,∠3和∠4,∠3和∠2,共4对. 故选C.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期末达标检测卷 题型:解答题
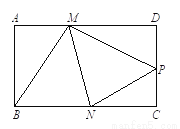
已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD与点M,折痕交边BC于点N .
(1)写出图中的全等三角形. 设CP= 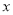 ,AM=
,AM= 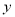 ,写出
,写出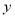 与
与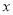 的函数关系式;
的函数关系式;
(2)试判断∠BMP是否可能等于90°. 如果可能,请求出此时CP的长;如果不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com