
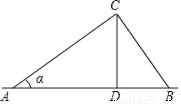
如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )
A. 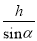 B.
B. 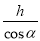 C.
C. 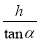 D.
D. 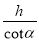
科目:初中数学 来源:江苏省苏州市姑苏区2017~2018学年第一学期八年级数学期末考试试卷 题型:单选题
点M(1,2)关于y轴对称点的坐标为( )
A.(﹣1,2) B.(﹣1,﹣2) C.(1,﹣2) D.(2,﹣1)
A 【解析】 试题分析:根据关于y轴对称的点,纵坐标相同,横坐标互为相反数解答. 【解析】 点M(1,2)关于y轴对称点的坐标为(﹣1,2). 故选A.查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB//OC,DC与OB交于点E则∠DEO的度数为( )
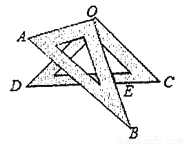
A. 85 B. 70
B. 70 C. 75
C. 75 D. 60
D. 60
查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
如图,在△ABC中,AB=AC,AH⊥BC,垂足为点H,如果AH=BC,那么sin∠BAC的值是_____.
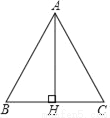
查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
如果抛物线y=2x2与抛物线y=ax2关于x轴对称,那么a的值是_____.
-2 【解析】根据关于x轴对称的抛物线的开口方向改变,开口大小不变,可由抛物线y=2x2与抛物线y=ax2关于x轴对称,知两抛物线开口大小不变,方向相反,因此可得a=﹣2. 故答案为:﹣2.查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:解答题
设函数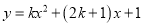 (
(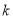 为实数)
为实数)
⑴.写出其中的两个特殊函数,使它们的图象不全是抛物线,并且在同一坐标系中,用描点法画出它们的图像;
⑵.根据所画图像,猜想出:对任意实数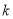 ,函数的图象都具有的特征,并给予证明;
,函数的图象都具有的特征,并给予证明;
⑶.对于任意负实数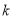 ,当
,当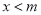 时,
时, 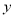 随
随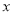 的增大而增大,试求
的增大而增大,试求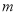 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:解答题
用配方法解方程: 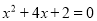
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:单选题
一元二次方程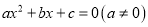 无实数根,则
无实数根,则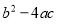 满足的条件是( )
满足的条件是( )
A. 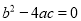 B.
B. 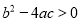 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第六章达标检测卷 题型:单选题
在数轴上表示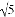 和-
和-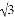 的两点间的距离是( )
的两点间的距离是( )
A. 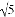 +
+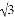 B.
B. 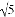 -
-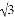 C. -(
C. -(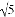 +
+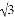 ) D.
) D. 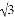 -
-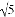
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com