
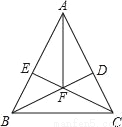
��ͼ���ڡ�ABC�У�AB=AC��BD��AC��D��CE��AB��E��BD��CE�ཻ��F��
��֤��AFƽ�֡�BAC��
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ������
�ⷽ�̣���3x+1��2=9x+3��
x1=����x2=�� �����������������������ʽ�ֽⷨ��һԪ���η��̼���. ������������������ã���3x+1��2��3��3x+1��=0�� �ֽ���ʽ�ã���3x+1����3x+1��3��=0�� �ɵ�3x+1=0��3x��2=0�� ��ã�x1=����x2=���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
����Ҫ�����������Ŀ��
��1��ͼ������ ����С�����壻
��2���������淽��ֽ�зֱ���������ͼ������ͼ����ͼ��
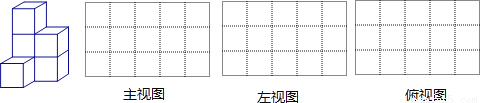
��3����С�������һ�����壬ʹ�����ĸ���ͼ������ͼ��������ͼ������������ͼһ�£��������ļ���������Ҫ�� �� ��С�����飬���Ҫ�� �� ��С�����飮
��1�� 6����2������������3��5�� 7�� �������������������1��ֱ�Ӹ�������ͼ�εó�С������ĸ����� ��2������ͼ��������С�����εĸ���Ϊ3��2������ͼ��������С�����εĸ���Ϊ3��1������ͼ��������С�����εĸ���Ϊ2��1�� ��3���ɸ���ͼ����ײ�С������ĸ�����������ͼ�ҵ�������������ٸ�������������Ӽ��ɣ� ��������� ��1�� 6 �� ��2����ͼ��ʾ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
����ͼ���в������۵�����������ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ������
��֪������x�Ķ��κ���y=x2+bx+c�����㣨��1��0���ͣ�2��6����
��1����b��c��ֵ��
��2������A��n��y1����B��n+1��y2����C��n+2��y3������������κ�����ͼ���ϣ����Ƿ��������n��ʹ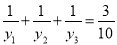 �������ڣ������n���������ڣ���˵�����ɣ�
�������ڣ������n���������ڣ���˵�����ɣ�
��3������P�Ƕ��κ���ͼ����y����ಿ���ϵ�һ�����㣬��ֱ��y=��2x��y������ƽ�ƣ��ֱ�x�ᡢy����C��D���㣬����CDΪֱ�DZߵġ�PCD���OCD���ƣ���������з���������P�����꣮
��1��b=1��c=0����2��n=2��5����3����P���꣨�������������� ���� �������������������1�����ô���ϵ�������ɽ�����⣮ ��2�����y1��y2��y3����ⷽ�̼��ɽ�����⣬ע�����㼼�ɣ� ��3����DΪֱ�Ƕ���ʱ����ͼ���֪�����ڵ�P��ʹ�á�PCDΪֱ�������Σ���CΪֱ�Ƕ��㣬CDΪֱ�DZ�ʱ����PE��OC��E������������CD=2PC����PC=2CD�� ��ֱ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ������
64��������Ϊ_____��
4 �����������������һ����x����������a����ôx��a�������������ݴ˶�����⼴�ɣ� �������� ��4����������64�� ��64������������4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
��������ı����ϻ�����ͼ1����ʾ�Ĵ��ߣ�ͼ2����չ��ͼ��ʾ��ͼ����ֻ��A���ϻ��д��ߣ���ô��ͼ1��ʣ���������еĴ�����ͼ2�У�������ȷ���ǣ����û���գ������Զ�����һ���ޣ�����������
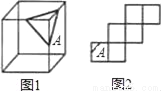
A. 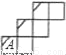 B.
B. 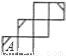 C.
C. 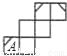 D.
D. 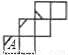
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʦ�����п���ѧ��ģ�Ծ� ���ͣ������
���� 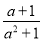 +
+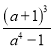 ��
��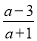 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�人���п���ѧģ���Ծ� ���ͣ������
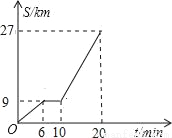
��ͼ��ʾ�Ƕ�������·�ڿ������������ij������ʻ��·��s��km����ʱ��t�����ӣ��ĺ�����ϵͼ���۲�ͼ�����ṩ����Ϣ������������⣺
��1��������ǰ6�����ڵ�ƽ���ٶ����� ��ǧ��/Сʱ���������˹�������ͣ�˶ʱ�䣿�� �����ӣ�
��2����10��t��20ʱ����S��t�ĺ�����ϵʽ��
��3���涨�����ٹ�·ʱ�ٳ���120ǧ��/СʱΪ������ʻ�����жϵ�10��t��20ʱ���������Ƿ��٣�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com