
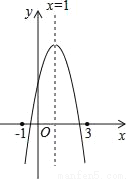
��ͼ�����κ���y=ax2+bx+c��ͼ����ʾ�����н����У���abc��0����2a+b=0���۵�m��1ʱ��a+b��am2+bm����a��b+c��0������ax12+bx1=ax22+bx2����x1��x2����x1+x2=2����ȷ�ĸ���Ϊ��������
A. 1�� B. 2�� C. 3�� D. 4��
C ���������������߿������£���a��0���������߶Գ���Ϊx= =1����b=��2a����b��0������������y��Ľ�����x���Ϸ�����c��0����abc��0�����Ԣٴ��� ��b=��2a����2a+b=0�����Ԣ���ȷ�� ��x=1ʱ������ֵ���a+b+c��am2+bm+c����a+b��am2+bm��m��1�������Ԣ���ȷ�� ����������x��Ľ��㵽�Գ���x=1�ľ������1������������x���һ... �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�������г�����2017-2018ѧ�����꼶���ϣ�������ѧ ���ͣ������
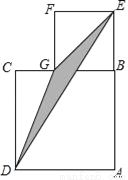
��ͼ��������ABCD��������BEFG����A��B��E��һֱ���ϣ���֪AB=a��BE=b��b��a����
��1����a��b�Ĵ���ʽ��ʾ��ADE�������
��2����a��b�Ĵ���ʽ��ʾ��DCG�������
��3����a��b�Ĵ���ʽ��ʾ��Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������2018����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ���ѡ��
��Rt��ABC�У���C=90�㣬��б���ϵĸ�Ϊh��sinA= �� ��AB�ij����ڣ�������
�� ��AB�ij����ڣ�������
A. 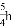 B.
B. 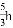 C.
C. 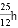 D.
D. 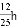
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�������п���ѧģ���Ծ������� ���ͣ������
���㣺����1����2+2sin245�㩁��1��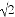 ��0
��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�������п���ѧģ���Ծ������� ���ͣ������
��֪|x|=5��y=3����x��y=__��
2��8 ����������Ϊ|x|=5 ����x=-5��x=5 ��x=5ʱ��y=3��x-y=2; ��x=-5ʱ��y=3��x-y=��8. ����x-y��2��x-y=-8. �ʴ��ǣ�2��-8.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�������п���ѧģ���Ծ������� ���ͣ���ѡ��
�������ʽ��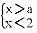 ǡ��3�������⣬��a��ȡֵ��Χ�ǣ�������
ǡ��3�������⣬��a��ȡֵ��Χ�ǣ�������
A. a�ܩ�1 B. a����1 C. ��2��a����1 D. ��2��a�ܩ�1
C ������������������߲���ʽǡ����3�������⣬ ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�������п���ѧģ���Ծ���ʮ�� ���ͣ������
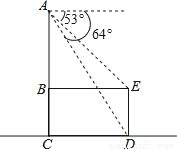
��ͼ�Ƿ���ˮƽ�����ϵ�һ�����ӵIJ���ͼ�����Ӹ�ΪAC�������ΪBE���νŸ�ΪED����AC��BE��AC��CD��AC��ED���ӵ�A��õ�D��E�ĸ��Ƿֱ�Ϊ64���53�㣮��֪ED=35cm�������Ӹ�ACԼΪ���٣�
���ο����ݣ�tan53��� ��sin53���
��sin53��� ��tan64���2��sin64���
��tan64���2��sin64��� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
�з��̽�Ӧ���⣺
����Ħ�г����������г�ͬʱ�����150ǧ������������У�����5Сʱ��������֪��ÿСʱ��ʻ��·������ÿСʱ��ʻ��·�̵�3����6ǧ�ף����������г����ٶ�.
�������г����ٶ�Ϊ9ǧ��/ʱ�� ��������������������⿼����һԪһ�η��̵�Ӧ��---�г����⣬���������г����ٶ�Ϊxǧ��/ʱ������ٶ�Ϊ��3x-6��ǧ��/ʱ���������������������ϵ�������������⼴�ɣ� �������� ���������г����ٶ�Ϊxǧ��/ʱ�� ������� 5(3x��6)+5x =150. ���x=9. ���������г����ٶ�Ϊ9ǧ��/ʱ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ������
һ�κ���y��kx��b��ͼ���㣨0��4������������������Χ�ɵ������ε����Ϊ8����k��_______��
1��-1 ����������һ�κ�����y�ύ�ڵ㣨0,4������b=4�� ��y=0ʱ����0=kx+4����x=����һ�κ�����x�ύ�ڵ㣨��0���� ����һ�κ���������������Χ�ɵ������ε����Ϊ=8�����k=��1. �ʴ�Ϊ1��-1.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com