
下列图形中,都是柱体的一组是( )
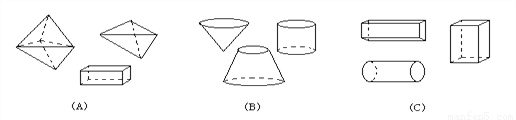
A. (A) B. (B) C. (C) D. 都不是
C 【解析】A选项中,因为只有1个几何体是柱体,另两个几何体中:一个是锥体,一个是不规则六面体,所以不能选A; B选项中,因为只有1个几何体是柱体,另两个几何体中:一个是锥体,一个是圆台,所以不能选B; C选项中,因为三个几何体都是柱体,所以可以选C; D选项中,因为C选项中的三个几何体都是柱体,所以D中说法错误; 故选C.科目:初中数学 来源:安徽省巢湖市2016-2017学年度第一学期七年级数期末教学质量检测 题型:解答题
大客车上原有(3a-b)人,中途一半人下车,又上车若干人,这时车上共有乘客(8a-5b)人,问上车乘客是多少人(用含a、b的代数式表示)?当a=10,b=8时,上车乘客是多少人?
6.5a-4.5b;29人 【解析】试题分析:原有人,中途下车人,又上车若干人后车上共有乘客人.中途上车乘客数=车上共有乘客数-中途下车人数,所以中途上车乘客为 ,把代入上式可得上车乘客人数. 试题解析:设上车乘客是人. 将代入其中得 答:上车乘客是29人.查看答案和解析>>
科目:初中数学 来源:甘肃省2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
下列计算正确的是( )
A. 3a+2a=5a2 B. 3a2-a2=3
C. 2a3+3a2=5a5 D. -a2b+2a2b=a2b
D 【解析】试题解析:A. 故错误. B. 故错误. C. 不是同类项不能合并. D.正确. 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级上学期第二次月考数学试卷 题型:填空题
服装店销售某款服装,标价为300元,若按标价的八折销售,仍可获利20%,则这款服装每件的进价是 ________元.
200 【解析】设这款服装每件进价为元,根据题意得: , 解得: . 即这款服装每件进价为200元.查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级上学期第二次月考数学试卷 题型:单选题
设P=2y-2,Q=2y+3,且3P-Q=1,则y的值是( )
A. 0.4 B. 2.5 C. -0.4 D. -2.5
B 【解析】∵P=2y-2,Q=2y+3,且3P-Q=1, ∴3(2y-2)-(2y+3)=1, 化简、整理得:4y-9=1,解得:y=2.5. 故选B.查看答案和解析>>
科目:初中数学 来源:山东省东营市2016-2017学年七年级上学期期中考试数学试卷 题型:解答题
如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=20°,求∠AOC的度数;
(2)若∠AOC:∠BOC=1:2,求∠EOD的度数.
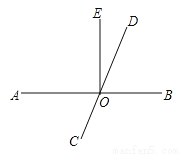
查看答案和解析>>
科目:初中数学 来源:山东省东营市2016-2017学年七年级上学期期中考试数学试卷 题型:填空题
如图在一块长为12cm,宽为6cm的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2cm),则空白部分表示的草地面积是_____________cm2。
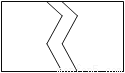
查看答案和解析>>
科目:初中数学 来源:北京101中学2017-2018学年上学期初中七年级期末考试数学试卷 题型:解答题
如图,∠AOB=90°,∠COD=90°,OE平分∠BOC,若∠1=30°,求∠COE的度数?
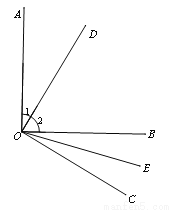
【解析】
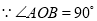
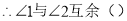
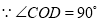
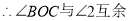

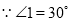
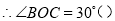
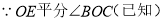
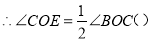
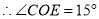
查看答案和解析>>
科目:初中数学 来源:陕西省西安市师大2017-2018学年初三期中考试数学试卷 题型:单选题
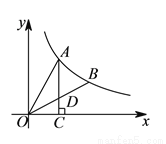
如图,  ,
,  是双曲线
是双曲线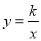 上的两点,过
上的两点,过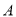 点作
点作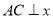 轴于点
轴于点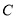 ,交
,交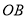 于点
于点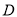 .若
.若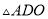 的面积为
的面积为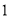 ,
, 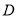 为
为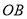 的中点,则
的中点,则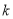 的值为( ).
的值为( ).
A. 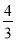 B.
B. 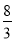 C.
C. 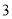 D.
D. 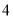
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com