
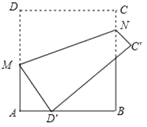
��ͼ����������ֽƬABCD��MN�۵���ʹ��D���ڱ�AB�ϣ���Ӧ��ΪD�䣬��C����C�䴦����AB=6��AD��=2�����ۺ�MN�ij�Ϊ ��
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���ຣʡ2017-2018ѧ�����꼶��ѧ��12���¿���ѧ�Ծ� ���ͣ������
д��һ��ϵ��Ϊ��5������ĸm��n�����ε���ʽΪ______����д��һ����
-5m2n �����������������ϵ��Ϊ?5,ֻ����ĸm��n�����ε���ʽΪ �ʴ�Ϊ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��̨�е�����������2017-2018ѧ��ȵ�һѧ�ڵ����νμ�����꼶��ѧ�Ծ� ���ͣ������
��1����֪a��b��Ϊ�෴����m��n��Ϊ������x�ľ���ֵΪ2����2mn+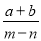 ��x2��ֵ��
��x2��ֵ��
��2����ͼ��ʾ������|a��c|+|a��b|+|c|

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��̨�е�����������2017-2018ѧ��ȵ�һѧ�ڵ����νμ�����꼶��ѧ�Ծ� ���ͣ���ѡ��
С���Ĵ��xԪ��С�ֵĴ���С����һ�뻹��2Ԫ��С�ֵĴ���ǣ�������
A. 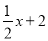 B.
B. 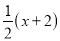 �� C.
�� C. 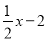 D.
D. 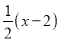
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
��ͼ����֪��O��ֱ��AB����CD���ഹֱ������Ϊ��E. ��O������BF����AD���ӳ����ཻ�ڵ�F����AD=3��cos��BCD=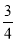 .
.
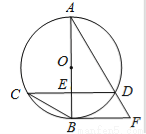
��1����֤��CD��BF��
��2�����O�İ뾶��
��3������CD�ij�.
��1����������2��2��3�� ���������������� ��1����BF�ǡ�O������ ��AB��BF ��������������1�� ��AB��CD ��CD��BF������������������������������������2�� ��2������BD ��AB��ֱ�� ���ADB=90�� ������������������������������3�� �ߡ�BCD=��BAD cos��BCD=��������������4�� ��cos��BAD= �֡�AD=3...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
�ֽ���ʽ��x2+4+4x��y2=_____��
��x+y+2����x��y+2�� �����������������ԭʽ �ʴ�Ϊ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
��ͼ��ֱ��AB��CD����1=50�㣬��2=110�㣬���E�Ĵ�С�ǣ� ��.
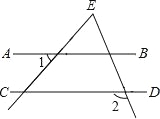
A��40�� B��50�� C��60�� D��30��
C�� �������� ����������ȸ���ƽ���ߵ����������3�Ķ������ٸ��������ε��������������ɣ���ͼ����AB��CD����1=50�㣬���3=��1=50�㣬�ߡ�2=110�㣬���E=��2����3=110�㩁50��=60�㣬��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
��1����ͼ1����һ���Ϊ12m����Ϊ20m�ľ��ε���������ͬ�����ĵ�·�����µIJ������ϲ�ƺ��Ҫʹ��ƺ�����Ϊ180m2�����·�Ŀ���
��2�����ڶԸþ���������и��죬��ͼ2���������뽨һ������εı���ƽ�е������ι���ͤ������ͤ���ı�������������εı���ƽ�е��ҿ�����ȵĵ�·����֪��·�Ŀ�Ϊ�����α߳���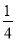 ������·�����ͤ�����֮���Ǿ��������
������·�����ͤ�����֮���Ǿ��������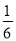 �����·�Ŀ���
�����·�Ŀ���
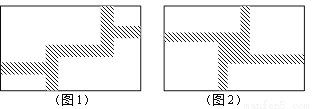
���𰸡���1����·��Ϊ2�ף���2����·�Ŀ�Ϊ1�ף�
�������������������1�����·��Ϊx�ף�����ƽ�ưѲ������ͼ�α�Ϊ����ͼ�Σ����һ�������в�ƺ���֮�;ͱ�Ϊ�ˣ�20��x����12��x����2�����������г����̣�����𰸣�
��2�����·�Ŀ�Ϊx�ף��������α߳�Ϊ4x�����ݵ�·�����ͤ�����֮���Ǿ��������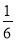 ���з�����⼴�ɣ�
���з�����⼴�ɣ�
�����������������
��1�����·��Ϊx�ף�
����������20��x����12��x��=180
��ã�x1=30����ȥ����x2=2
�𣺵�·��Ϊ2�ף�
��2�����·�Ŀ�Ϊx�ף�
����з��̣�x��12-4x��+x��20-4x��+16x2=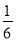 ��20��12��
��20��12��
����x2+4x-5=0��
��ã�x1=1��x2=-5����ȥ����
�𣺵�·�Ŀ�Ϊ1�ף�
�㾦��������һԪ���η��̵�Ӧ�ã�������Ŀ���������ν�ϵ�˼�룬������ƽ�ưѲ������ͼ�α�Ϊ����ͼ�Σ����������г����̣�����𰸣����Ҫע���ĺ����ԣ��Ӷ�ȷ��ȡ�ᣮ
�����͡������
��������
10
��ͼ1��һ����������װ�У����ĵ����DZ߳�Ϊ10cm���������Σ��������涼�Ǿ��Σ��ֽ���Ϊ15cm�IJ�ɫ����ֽ��AMCN�ü���һ��ƽ���ı���ABCD����ͼ2����Ȼ��������ƽ���ı���ֽ������ͼ3�ķ�ʽ�������������װ�еIJ�����а�����Ҫ�����ʱû���ص����֣���ֽ���ڲ��������Ȧ�����ý������������װ�еIJ���ȫ������������ͼ3�У����������ع���A�IJ���������õ���ͼ4�IJ���չ��ͼ.Ϊ�˵õ��ü��ĽǶ�,���ǿ��Ը���չ��ͼƴ�ӳ�����������ƽ���ı��ν����о�.

��1������ͼ4�л���ƴ�Ӻ����������ƽ���ı��Σ�
��2������ͼ2�У�����ü��ĽǶȣ�����ABM�Ķ�����.
��1����ͼ����������2����ABM=30�㣮 ����������������1����ͼ4�еġ�ABE����ƽ��30cm����CDF����ƽ��30cm��ƴ����ͼ�е�ƽ���ı��Σ���ƽ���ı��μ�Ϊͼ2�е��ı���ABCD�� ��2���������������AB=30cm����ֽ���Ŀ�Ϊ15cm���������Ǻ�����á�AMB=30�㣮 �����������1����ͼ�� ��2����ͼ2�İ�������֪��AB�ij������������ĵױ��ܳ�����AB=3...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���A���� ���ͣ������
Ϊ���衰������塱����Ҫ��ij����������ˮ�ܽ��и��죬�ù������ɼӵ���ʩ��ǡ���ڹ涨ʱ������ɣ������Ҷӵ���ʩ��������ɹ�������ʱ���ǹ涨������1.5������ɼס��������Ⱥ���10�죬��ô���µĹ������Ҷӵ�����ɻ���5�죮
(1)�������ɹ涨��ʱ���Ƕ����죿
(2)��֪��ÿ���ʩ������Ϊ6500Ԫ���Ҷ�ÿ���ʩ������Ϊ3600Ԫ��Ϊ�����̹����Լ��ٶԾ�����ˮ��Ӱ�죬����ָ�Ӳ����վ����ù����ɼס������Ӻ�������ɣ���ù���ʩ�������Ƕ��٣�
(1)20��;(2) 121200Ԫ ����������������� ��1����涨ʱ��Ϊ�죬��ӵ�������Ҫ�죬�Ҷӵ�������Ҫ�죬�ɡ����Ӻ���10�죬�����Ҷӵ�����5������ȫ�����̡����г����̣��ⷽ�̼�����ù涨ʱ�䣻 ��2���ɣ�1�����������ɵüס������Ӹ��ԵĹ���Ч�ʣ��ɴ˿ɼ�������Ӻ������ȫ����������ʱ�䣬��ϡ���ÿ���ʩ������Ϊ6500Ԫ���Ҷ�ÿ���ʩ������Ϊ3600Ԫ�����ɼ�...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com