
ШчЭМЃЌвбжЊЁбOЕФжБОЖABгыЯвCDЛЅЯрДЙжБЃЌДЙзуЮЊЕуE. ЁбOЕФЧаЯпBFгыЯвADЕФбгГЄЯпЯрНЛгкЕуFЃЌЧвAD=3ЃЌcosЁЯBCD=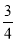 .
.
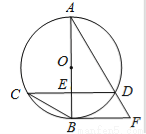
ЃЈ1ЃЉЧѓжЄЃКCDЁЮBFЃЛ
ЃЈ2ЃЉЧѓЁбOЕФАыОЖЃЛ
ЃЈ3ЃЉЧѓЯвCDЕФГЄ.
ЃЈ1ЃЉМћНтЮіЃЈ2ЃЉ2ЃЈ3ЃЉ ЁОНтЮіЁПЁОНтЮіЁП ЃЈ1ЃЉЁпBFЪЧЁбOЕФЧаЯп ЁрABЁЭBF ЁЁЁЁЁЁЁ1Зж ЁпABЁЭCD ЁрCDЁЮBFЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁ2Зж ЃЈ2ЃЉСЌНсBD ЁпABЪЧжБОЖ ЁрЁЯADB=90Ёу ЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁ3Зж ЁпЁЯBCD=ЁЯBAD cosЁЯBCD=ЁЁЁЁЁЁЁ4Зж ЁрcosЁЯBAD= гжЁпAD=3... аЧМЖПкЫуЬьЬьСЗЯЕСаД№АИ
аЧМЖПкЫуЬьЬьСЗЯЕСаД№АИ УЂЙћНЬИЈДяБъВтЪдОэЯЕСаД№АИ
УЂЙћНЬИЈДяБъВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЧрКЃЪЁ2017-2018бЇФъЦпФъМЖЩЯбЇЦк12дТдТПМЪ§бЇЪдОэ ЬтаЭЃКЬюПеЬт
Шє2aЉb=3ЃЌдђЖрЯюЪН8aЉ4b+3ЕФжЕЪЧ______ЃЎ
15 ЁОНтЮіЁПЪдЬтНтЮіЃК ЙЪД№АИЮЊЃКВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКНЫеЪЁЖЋЬЈЪаЕкШ§НЬг§СЊУЫ2017-2018бЇФъЖШЕквЛбЇЦкЕкШ§ДЮНзЖЮМьВтЦпФъМЖЪ§бЇЪдОэ ЬтаЭЃКНтД№Ьт
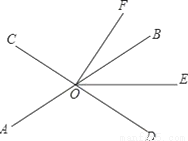
ШчЭМЃЌжБЯпABЁЂCDЯрНЛгкЕуOЃЌOEЦНЗжЁЯBODЃЎ
ЃЈ1ЃЉШєЁЯAOC=70ЁуЃЌЁЯDOF=90ЁуЃЌЧѓЁЯEOFЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєOFЦНЗжЁЯCOEЃЌЁЯBOF=15ЁуЃЌШєЩшЁЯAOE=xЁуЃЎ
ЂйгУКЌxЕФДњЪ§ЪНБэЪОЁЯEOF;
ЂкЧѓЁЯAOCЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКНЫеЪЁЖЋЬЈЪаЕкШ§НЬг§СЊУЫ2017-2018бЇФъЖШЕквЛбЇЦкЕкШ§ДЮНзЖЮМьВтЦпФъМЖЪ§бЇЪдОэ ЬтаЭЃКЬюПеЬт
ШєЕЅЯюЪН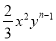 гыЕЅЯюЪНЉ5xmy3ЪЧЭЌРрЯюЃЌдђmЉnЕФжЕЮЊ________ЃЎ
гыЕЅЯюЪНЉ5xmy3ЪЧЭЌРрЯюЃЌдђmЉnЕФжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКНЫеЪЁЖЋЬЈЪаЕкШ§НЬг§СЊУЫ2017-2018бЇФъЖШЕквЛбЇЦкЕкШ§ДЮНзЖЮМьВтЦпФъМЖЪ§бЇЪдОэ ЬтаЭЃКЕЅбЁЬт
ЯТСаИїЪНЃКЂйЉЃЈЉ2ЃЉЃЛЂкЉ|Љ2|ЃЛЂлЉ22ЃЛЂмЉЃЈЉ2ЃЉ2ЃЌМЦЫуНсЙћЮЊИКЪ§ЕФИіЪ§гаЃЈ ЃЉ.
A. 4Иі B. 3Иі C. 2Иі D. 1Иі
B ЁОНтЮіЁПЁпЂйЃ(Ѓ2)=2>0ЃЛЂкЃ|Ѓ2|=-2<0ЃЛЂлЃ22=-4<0ЃЛЂмЃ(Ѓ2)2=-4<0; ЁрМЦЫуНсЙћЮЊИКЪ§ЕФИіЪ§га3ИіЁЃ ЙЪбЁB.ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2017ФъЙѓжнЪЁжаПМЪ§бЇЖўФЃЪдОэ ЬтаЭЃКЬюПеЬт
ШчЭМЃЌНЋе§ЗНаЮжНЦЌABCDбиMNелЕўЃЌЪЙЕуDТфдкБпABЩЯЃЌЖдгІЕуЮЊDЁфЃЌЕуCТфдкCЁфДІЃЎШєAB=6ЃЌADЁф=2ЃЌдђелКлMNЕФГЄЮЊ ЃЎ
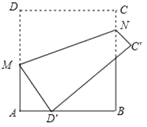
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2017ФъЙѓжнЪЁжаПМЪ§бЇЖўФЃЪдОэ ЬтаЭЃКЕЅбЁЬт
ХзЮяЯпЭМЯѓШчЭМЫљЪОЃЌИљОнЭМЯѓЃЌХзЮяЯпЕФНтЮіЪНПЩФмЪЧЃЈЁЁЁЁЃЉ
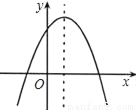
A. y=x2Љ2x+3 B. y=Љx2Љ2x+3 C. y=Љx2+2x+3 D. y=Љx2+2xЉ3
C ЁОНтЮіЁПЪдЬтНтЮіЃКгЩЭМЯѓЕУЃКa<0ЃЌb>0ЃЌc>0. ЙЪбЁC.ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЛЦН№30ЬтЯЕСа ОХФъМЖЪ§бЇ ДѓЬтвзЖЊЗж ЬтаЭЃКНтД№Ьт
ШчЭМЃЌдк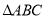 жаЃЌ
жаЃЌ 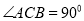 ЃЌЕу
ЃЌЕу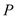 ЕН
ЕН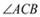 СНБпЕФОрРыЯрЕШЃЌЧв
СНБпЕФОрРыЯрЕШЃЌЧв ЃЎ
ЃЎ
ЃЈ1ЃЉЯШгУГпЙцзїГіЗћКЯвЊЧѓЕФЕу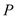 ЃЈБЃСєзїЭМКлМЃЃЌВЛашвЊаДзїЗЈЃЉЃЌШЛКѓХаЖЯЁїABPЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈБЃСєзїЭМКлМЃЃЌВЛашвЊаДзїЗЈЃЉЃЌШЛКѓХаЖЯЁїABPЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЩш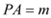 ЃЌ
ЃЌ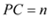 ЃЌЪдгУ
ЃЌЪдгУ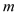 ЁЂ
ЁЂ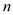 ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО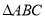 ЕФжмГЄКЭУцЛ§ЃЛ
ЕФжмГЄКЭУцЛ§ЃЛ
ЃЈ3ЃЉЩш гы
гы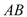 НЛгкЕу
НЛгкЕу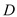 ЃЌЪдЬНЫїЕББп
ЃЌЪдЬНЫїЕББп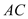 ЁЂ
ЁЂ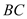 ЕФГЄЖШБфЛЏЪБЃЌ
ЕФГЄЖШБфЛЏЪБЃЌ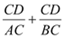 ЕФжЕЪЧЗёЗЂЩњБфЛЏЃЌШєВЛБфЃЌЪдЧѓГіетИіВЛБфЕФжЕЃЌШєБфЛЏЃЌЪдЫЕУїРэгЩЃЎ
ЕФжЕЪЧЗёЗЂЩњБфЛЏЃЌШєВЛБфЃЌЪдЧѓГіетИіВЛБфЕФжЕЃЌШєБфЛЏЃЌЪдЫЕУїРэгЩЃЎ
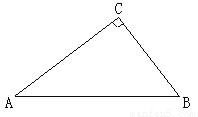
ЁОД№АИЁП(1)зїЭММћНтЮіЃЛІЄABPЪЧЕШбќжБНЧШ§НЧаЮ. РэгЩМћНтЮіЃЛЃЈ2ЃЉ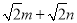 ЃЛ
ЃЛ 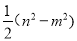 ЃЈ3ЃЉ
ЃЈ3ЃЉ .
.
ЁОНтЮіЁП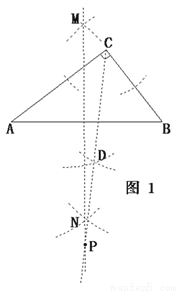 ЃЈ1ЃЉвРЬтвтЃЌЕуPМШдк
ЃЈ1ЃЉвРЬтвтЃЌЕуPМШдк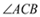 ЕФЦНЗжЯпЩЯЃЌ
ЕФЦНЗжЯпЩЯЃЌ
гждкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯ.
ШчЭМ1ЃЌзї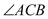 ЕФЦНЗжЯп
ЕФЦНЗжЯп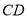 ЃЌ
ЃЌ
зїЯпЖЮ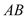 ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп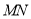 ЃЌ
ЃЌ 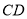 гы
гы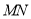 ЕФ
ЕФ
НЛЕуМДЮЊЫљЧѓЕФPЕуЁЃЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈ3Зж
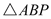 ЪЧЕШбќжБНЧШ§НЧаЮ.
ЪЧЕШбќжБНЧШ§НЧаЮ.
РэгЩЃКЙ§ЕуPЗжБ№зї ЁЂ
ЁЂ ЃЌДЙзуЮЊEЁЂFШчЭМ2.
ЃЌДЙзуЮЊEЁЂFШчЭМ2.
Ёп ЦНЗж
ЦНЗж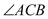 ЃЌ
ЃЌ ЁЂ
ЁЂ ЃЌДЙзуЮЊEЁЂFЃЌ
ЃЌДЙзуЮЊEЁЂFЃЌ
Ёр .
.
гжЁп  ЃЌЁр
ЃЌЁр  Ёе
Ёе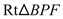 .ЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈ4Зж
.ЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈ4Зж
Ёр  .
.
Ёп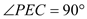 ЃЌ
ЃЌ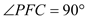 ЃЌ
ЃЌ ЃЌ
ЃЌ
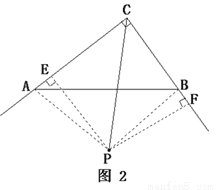 Ёр
Ёр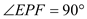 ЃЌ ДгЖј
ЃЌ ДгЖј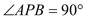 .
.
гж Ёр
Ёр 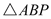 ЪЧЕШбќжБНЧШ§НЧаЮ. ЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈ5Зж
ЪЧЕШбќжБНЧШ§НЧаЮ. ЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈ5Зж
ЃЈ2ЃЉШчЭМ2ЃЌдк жаЃЌ
жаЃЌ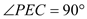 ЃЌ
ЃЌ
 ЃЌ
ЃЌ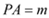 . Ёр
. Ёр .
.
гЩ Ёе
Ёе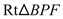 ЃЌ
ЃЌ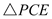 Ёе
Ёе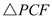 ЃЌ
ЃЌ
ПЩЕУ ЃЌ
ЃЌ .
.
Ёр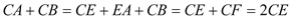 .
.
дк жаЃЌ
жаЃЌ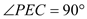 ЃЌ
ЃЌ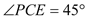 ЃЌ
ЃЌ ЃЌ
ЃЌ
Ёр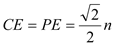 . Ёр
. Ёр . ЉЈЉЈЉЈЉЈ6Зж
. ЉЈЉЈЉЈЉЈ6Зж
Ыљвд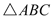 ЕФжмГЄЮЊЃК
ЕФжмГЄЮЊЃК . ЉЈЉЈЉЈЉЈ7Зж
. ЉЈЉЈЉЈЉЈ7Зж
вђЮЊ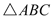 ЕФУцЛ§=
ЕФУцЛ§=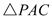 ЕФУцЛ§
ЕФУцЛ§
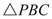 ЕФУцЛ§
ЕФУцЛ§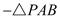 ЕФУцЛ§
ЕФУцЛ§
=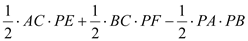 =
=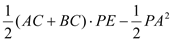
=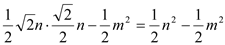 ЃЈ
ЃЈ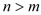 ЃЉЉЈЉЈ9Зж
ЃЉЉЈЉЈ9Зж
Лђ 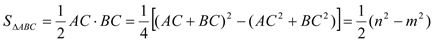 .
.
ЃЈ3ЃЉЙ§Еу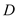 ЗжБ№зї
ЗжБ№зї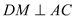 ЁЂ
ЁЂ ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ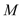 ЁЂ
ЁЂ ШчЭМ3.
ШчЭМ3.
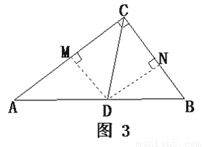 Ёп
Ёп 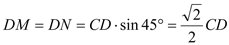 .ЉЈЉЈЉЈЉЈ10Зж
.ЉЈЉЈЉЈЉЈ10Зж
гЩ ЁЮ
ЁЮ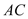 ЕУ
ЕУ 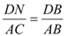 ЂйЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈ11Зж
ЂйЉЈЉЈЉЈЉЈЉЈЉЈЉЈЉЈ11Зж
гЩ ЁЮ
ЁЮ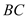 ЕУ
ЕУ 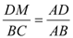 Ђк ЉЈЉЈЉЈЉЈЉЈЉЈ12Зж
Ђк ЉЈЉЈЉЈЉЈЉЈЉЈ12Зж
Ђй+ЂкЃЌЕУ 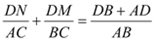 ЃЌМД
ЃЌМД 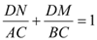 .
.
Ёр 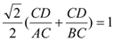 ЃЌ МД
ЃЌ МД 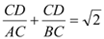 ЉЈЉЈЉЈЉЈ13Зж
ЉЈЉЈЉЈЉЈ13Зж
ЁОЕуОІЁПЃЈ1ЃЉгЩЬтвтзїГіЁЯACBЕФНЧЦНЗжЯпКЭЯпЖЮABЕФДЙжБЦНЗжЯпПЩЧѓГіЕуPЃЌШЛКѓжЄУїRtЁїAPEЁеRtЁїBPFМДПЩЃЛ
ЃЈ2ЃЉгЩPA=PBЃЌPA=mЃЌПЩЕУГі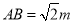 ЃЌгЩRtЁїAPEЁеRtЁїBPFЃЌЁїPCEЁеЁїPCFЃЌПЩЕУCA+CB=CE+EA+CB=CE+CF=2CEЃЌдкRtЁїPCEжаЃЌ PC=nЃЌПЩжЊ
ЃЌгЩRtЁїAPEЁеRtЁїBPFЃЌЁїPCEЁеЁїPCFЃЌПЩЕУCA+CB=CE+EA+CB=CE+CF=2CEЃЌдкRtЁїPCEжаЃЌ PC=nЃЌПЩжЊ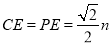 ЃЌМД
ЃЌМД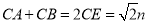 ЃЌзюКѓЧѓГіжмГЄКЭУцЛ§ЃЛ
ЃЌзюКѓЧѓГіжмГЄКЭУцЛ§ЃЛ
ЃЈ3ЃЉгЩЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЕУЕН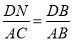 ,
, 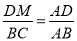 ЪЧНтД№БОЬтЕФЙиМќЃЎ
ЪЧНтД№БОЬтЕФЙиМќЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
15
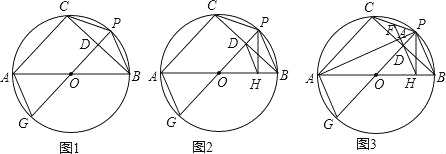
ЁбOЪЧЁїABCЕФЭтНгдВЃЌABЪЧжБОЖЃЌЙ§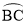 ЕФжаЕуPзїЁбOЕФжБОЖPGЃЌгыЯвBCЯрНЛгкЕуDЃЌСЌНгAGЁЂCPЁЂPBЃЎ
ЕФжаЕуPзїЁбOЕФжБОЖPGЃЌгыЯвBCЯрНЛгкЕуDЃЌСЌНгAGЁЂCPЁЂPBЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКAG=CPЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуPзїABЕФДЙЯпЃЌДЙзуЮЊЕуHЃЌСЌНгDHЃЌЧѓжЄЃКDHЁЮAGЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌСЌНгPAЃЌбгГЄHDЗжБ№гыPAЁЂPCЯрНЛгкЕуKЁЂFЃЌвбжЊFK=2ЃЌЁїODHЕФУцЛ§ЮЊ2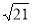 ЃЌЧѓACЕФГЄЃЎ
ЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЛЦН№30ЬтЯЕСа ЦпФъМЖЪ§бЇ аЁЬтвзЖЊЗж ЬтаЭЃКЕЅбЁЬт
ШчЭМЃЌЯТСаЫЕЗЈВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
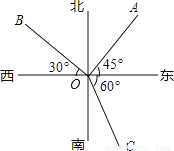
A. OCЕФЗНЯђЪЧФЯЦЋЖЋ30Ёу B. OAЕФЗНЯђЪЧББЦЋЖЋ45Ёу
C. OBЕФЗНЯђЪЧЮїЦЋББ30Ёу D. ЁЯAOBЕФЖШЪ§ЪЧ75Ёу
D ЁОНтЮіЁПНтЃКAЃЎ OCЕФЗНЯђЪЧФЯЦЋЖЋ30Ёу ЃЌе§ШЗЃЛ BЃЎ OAЕФЗНЯђЪЧББЦЋЖЋ45ЁуЃЌе§ШЗЃЛ CЃЎ OBЕФЗНЯђЪЧЮїЦЋББ30Ёу ЃЌе§ШЗЃЛ DЃЎ ЁЯAOBЕФЖШЪ§ЪЧ180Ёу-75Ёу=105ЁуЃЌДэЮѓЃЎ ЙЪбЁDЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com