
下列说法:①平面内过一点有且只有一条直线和已知直线垂直;②垂线段最短;③平行于同一条直线的两条直线也互相平行;④同位角相等.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】①平面内过一点有且只有一条直线和已知直线垂直,正确;②垂线段最短,正确 ;③平行于同一条直线的两条直线也互相平行,正确;④同位角相等,错误,只有两直线平行,才有同位角相等, 所以正确的说法有3个, 故选C.科目:初中数学 来源:重庆市江津区2016-2017学年七年级下学期期末考试数学试卷 题型:单选题
小红家的冰箱冷藏室温度是 ℃,冷冻室的温度是
℃,冷冻室的温度是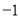 ℃,则她家的冰箱冷藏室比冷冻室温度高( )
℃,则她家的冰箱冷藏室比冷冻室温度高( )
A. 2 ℃
B. -2 ℃
C. 4 ℃
D. -4 ℃
C 【解析】由题意可得:3-(-1)=3+1=4(℃). 故选C.查看答案和解析>>
科目:初中数学 来源:2017年海南省文昌市中考数学模拟试卷 题型:单选题
如图,已知AB⊥GH,CD⊥GH,直线CD,EF,GH相交于一点O,若∠1=42°,则∠2等于( )
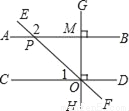
A. 130° B. 138° C. 140° D. 142°
B 【解析】试题解析:如图: ∵AB⊥GH,CD⊥GH, ∴∠GMB=∠GOD=90°, ∴AB∥CD, ∴∠BPF=∠1=42°, ∴∠2=180°-∠BPF=180°-42°=138°, 故选B.查看答案和解析>>
科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:解答题
如图所示,已知AD∥BC,且DC⊥AD于D.
(1)DC与BC有怎样的位置关系?说说你的理由;
(2)你能说明∠1+∠2=180°吗?
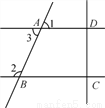
查看答案和解析>>
科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:填空题
如图,已知AB∥CD,∠1=120°,则∠C=____.
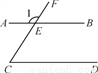
查看答案和解析>>
科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:单选题
下列计算正确的是 ( )
A. a5+a5=a10 B. a3·a2=a6 C. a7÷a=a6 D. (-a3)2=-6a6
C 【解析】A. a5+a5=2a5 ,故A选项错误;B. a3·a2=a5 ,故B选项错误;C. a7÷a=a6 ,正确;D. (-a3)2=a6,故D选项错误, 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
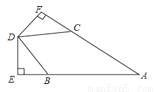
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
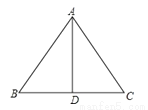
A. 35° B. 45° C. 55° D. 60°
C 【解析】试题分析:由等腰三角形的三线合一性质可知∠BAC=70°,再由三角形内角和定理和等腰三角形两底角相等的性质即可得出结论. 【解析】 AB=AC,D为BC中点, ∴AD是∠BAC的平分线,∠B=∠C, ∵∠BAD=35°, ∴∠BAC=2∠BAD=70°, ∴∠C=(180°﹣70°)=55°. 故选C.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
等腰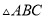 的周长为
的周长为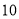 ,则其腰长
,则其腰长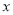 的取值范围是( ).
的取值范围是( ).
A. 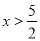 B.
B. 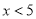 C.
C. 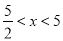 D.
D. 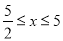
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com