练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

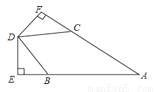
    已知，如图所示，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．

    证明见解析. 【解析】试题分析：连接AD，利用“边边边”证明△ABD和△ACD全等，然后根据全等三角形对应角相等可得∠BAD=∠CAD，再根据角平分线上的点到角的两边距离相等证明即可． 试题解析：证明：连接AD， 在△ACD和△ABD中， AC=AB，CD=BD，AD=AD ∴△ACD≌△ABD（SSS）， ∴∠EAD=∠FAD，即AD平分∠EAF， ∵D...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年山西农业大学附中七年级（下）第二次月考数学试卷 题型：填空题

    若代数式y2﹣2y+3的值为6，那么代数式﹣2y2+4y﹣5的值为_____．

    ﹣11 【解析】试题解析：∵y2-2y+3=6 ∴y2-2y=3 ∴-2y2+4y-5=-2（y2-2y）-5=-6-5=-11.

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省文昌市中考数学模拟试卷 题型：单选题

    ﹣8的相反数是（　　）

    A. ﹣8 B. 8 C. -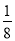 D.

    B 【解析】试题分析：直接根据相反数的定义进行解答即可．由相反数的定义可知，﹣8的相反数是﹣（﹣8）=8． 故选：B．

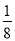
    查看答案和解析>>

    科目：初中数学 来源：2018年春北师大版七年级数学下册活页测试卷：期末测试 题型：单选题

    下列说法：①平面内过一点有且只有一条直线和已知直线垂直；②垂线段最短；③平行于同一条直线的两条直线也互相平行；④同位角相等.其中正确的有( )

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】①平面内过一点有且只有一条直线和已知直线垂直，正确；②垂线段最短，正确 ；③平行于同一条直线的两条直线也互相平行，正确；④同位角相等，错误，只有两直线平行，才有同位角相等， 所以正确的说法有3个， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

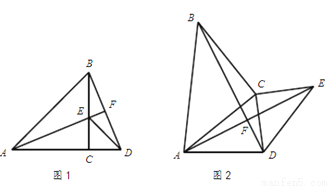
    在△ABC和△DEC中，AC=BC，DC=EC，∠ACB=∠ECD=90°．

    （1）如图1，当点A、C、D在同一条直线上时，AC=12，EC=5，

    ①求证：AF⊥BD； ②求AF的长度；

    （2）如图2，当点A、C、D不在同一条直线上时，求证：AF⊥BD.

    （1）①证明见解析；②；（2）证明见解析. 【解析】试题分析：（1）①证明△ACE≌△BCD，得到∠1=∠2，由对顶角相等得到∠3=∠4，所以∠BFE=∠ACE=90°，即可得结论；②根据勾股定理求出BD，利用△ABD的面积的两种表示方法，即可解答；（2）证明△ACE≌△BCD，得到∠1=∠2，又由∠3=∠4，得到∠BFA=∠BCA=90°，即可得结论. 试题解析： （1）①证明...

    查看答案和解析>>

    科目：初中数学 来源：江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

    尺规作图：如图，在四边形ABCD内找一点P，使得点P到AB、AD的距离相等，并且点P到点B、C的距离也相等．（不写作法，保留作图痕迹）．

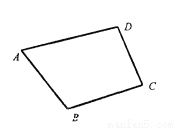
    作图见解析. 【解析】试题分析：利用角平分线的作法作出∠A的平分线，再作出线段BC的垂直平分线，这两条平分线的交点即为点P的位置． 试题解析：

    查看答案和解析>>

    科目：初中数学 来源：江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型：填空题

    如果等腰三角形的顶角等于50°，那么它的底角为______________°．

    65 【解析】根据等腰三角形两底角相等，三角形内角和是180度，可得等腰三角形一个底角的度数为 .故答案为：65°．

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学模拟试卷 题型：填空题

    布袋中装有2个红球，3个白球，5个黑球，它们除颜色外均相同，则从袋中任意摸出一个球是白球的概率是_____．

    0.3 【解析】试题解析：∵布袋中装有2个红球，3个白球，5个黑球，共10个球，从袋中任意摸出一个球共有10种结果，其中出现白球的情况有3种可能， ∴是白球的概率是 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型：解答题

    某港口位于东西方向的海岸线上．“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后相距30海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行？为什么？

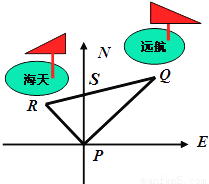
    “海天”号沿西北方向航行 【解析】试题分析：根据路程=速度×时间分别求得PQ、PR的长，再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形，从而求解． 试题解析：根据题意，得 PQ=16×1.5=24（海里），PR=12×1.5=18（海里），QR=30（海里）． ∵242+182=302 ， 即PQ2+PR2=QR2 ， ∴∠QPR=90°． ...

    查看答案和解析>>

    同步练习册答案