
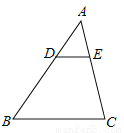
如图,在△ABC中,若DE∥BC,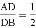 ,DE=4cm,则BC的长为___________.
,DE=4cm,则BC的长为___________.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源:广西北海市银海区2017年秋季学期教学质量监测七年级数学试卷 题型:填空题
一个多项式加上2x 2-4x-3得x 2 -3x,则这个多项式为_______________ .
-x2+x+3 【解析】【解析】 设多项式为A.由题意得: A=(﹣x2﹣3x)﹣(2x2﹣4x﹣3)=﹣3x2+x+3.故答案为:﹣3x2+x+3.查看答案和解析>>
科目:初中数学 来源:河南省新乡市卫辉市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
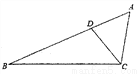
如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点F(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:河南省新乡市卫辉市2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
若直角三角形的三边a、b、c满足a2-4a+4+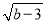 =0,则第三边c的长度是( )
=0,则第三边c的长度是( )
A. 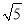 B.
B. 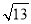 C.
C. 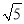 或
或 D. 5或13
D. 5或13
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第27章 相似 单元检测卷 题型:填空题
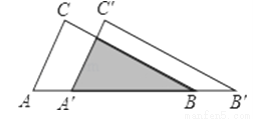
如图,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB=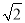 , 则此三角形移动的距离AA′=________ .
, 则此三角形移动的距离AA′=________ .
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第27章 相似 单元检测卷 题型:单选题
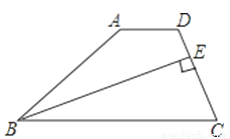
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第27章 相似 单元检测卷 题型:单选题
如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为( )

A.  B.
B.  C. 2 D. 3
C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学第一、二章综合测试卷 题型:填空题
若一个三角形的外角平分线与三角形的一边平行,则这个三角形是 ________三角形.
等腰 【解析】试题解析:如图, DC平分∠ACE,且AB∥CD, ∴∠ACD=∠DCE,∠A=∠ACD,∠B=∠DCE ∴∠B=∠A, ∴△ABC为等腰三角形. 故答案为:等腰.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 2.1 两条直线的位置关系(1) 同步练习 题型:填空题
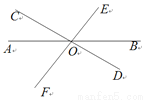
如图,直线AB、CD、EF相交于点O,∠AOD=150°,∠DOE=80°,则∠AOF=____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com