
请你参与亮亮在翻转扑克牌游戏时的思考.
(1)亮亮同学把3张正面都朝上的扑克牌每次都翻转2张,改变它们的朝向.他发现无论经过多少次这样的操作都不能使3张扑克牌的正面全部朝下.他的结论对吗?
(2)把4张正面都朝上的扑克牌每次都翻转2张,改变它们朝向,经过若干次操作,能否使4张扑克牌的正面都朝下呢?
(3)把4张正面都朝上的扑克牌每次都翻转3张,改变它们朝向,经过若干次操作,能否使4张扑克牌的正面都朝下呢?若能,至少要经过几次这样的操作?若不能,请说明理由.
(1)正确(2)能(3)能,至少4次 【解析】试题分析:(1)根据3个奇数的和是奇数,所以翻动的总张数为奇数时,才能使3张牌的牌面都向下,而每次翻动2张,不管翻多少次,翻动的总张数都是偶数,进而得出答案; (2)根据4个奇数的和是偶数,所以翻动的总张数为偶数时,才能使4张牌的牌面都向下,而每次翻动2张,故翻动的总张数都是偶数,进而得出答案; (3)可以试验一下,只有将一张牌翻动奇... 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:单选题
如图,在直角坐标系中,⊙O的半径为1,则直线y=﹣2x+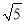 与⊙O的位置关系是( )
与⊙O的位置关系是( )
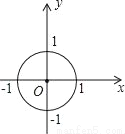
A. 相离 B. 相交 C. 相切 D. 无法确定
C 【解析】原点到直线的距离=1,所以直线与⊙O的位置关系是相切。故选C查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
旋转后能与自身重合,旋转有最小的图形是( ).
A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形
D 【解析】分析:确定正三角形,矩形,正五边形,正六边形四个图形,各绕自己的中心最少旋转多少度可与自身重合,就是观察图形,可以被从中心发出的射线平分成几部分,则旋转的最小角度即可求解,从而进行选择. 解答:【解析】 A、正三角形旋转的最小的能与自身重合的度数是120度; B、矩形旋转的最小的能与自身重合的度数是180度; C、正五边形旋转的最小的能与自身重合的度数是72度...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:单选题
如果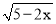 是二次根式,那么x应满足的条件是( )
是二次根式,那么x应满足的条件是( )
A. 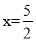 B.
B. 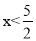 C.
C. 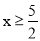 D.
D. 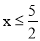
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.
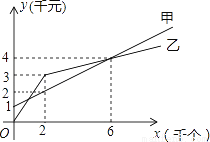
(1)填空:甲厂的制版费是________千元,当x≤2(千个)时乙厂证书印刷单价是________元/个;
(2)求出甲厂的印刷费y甲与证书数量x的函数关系式,并求出其证书印刷单价;
(3)当印制证书8千个时,应选择哪个印刷厂节省费用,节省费用多少元?
(1)1;1.5(2)y=0.5x+1(3)选择乙厂节省费用,节省费用500元 【解析】试题分析:(1)根据纵轴图象判断即可,用2到6千个时的费用除以证件个数计算即可得解;(2)设甲厂的印刷费y甲与证书数量x的函数关系式为y=kx+b,利用待定系数法解答即可;(3)用待定系数法求出乙厂x>2时的函数解析式,再求出x=8时的函数值,再求出甲厂印制1个的费用,然后求出8千个的费用,比较即可得解....查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
如图,分别以Rt△ABC的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是________.
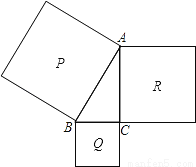
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
一个三角形的两边长分别为3 cm和7 cm,则此三角形的第三边的长可能是( )
A. 3 cm B. 4 cm C. 7 cm D. 11 cm
C 【解析】试题解析:设第三边长为xcm,根据三角形的三边关系可得: 7-3<x<7+3, 解得:4<x<10, 故答案为C.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= ___________度
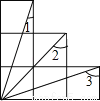
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:解答题
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2﹣10x+16=0的两个根,且抛物线的对称轴是直线x=﹣2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com