
已知点A(-1,y1),B(2,y2)都在双曲线y=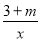 上,且y1>y2,则m的取值范围是( )
上,且y1>y2,则m的取值范围是( )
A. m<0 B. m>0 C. m>-3 D. m<-3
D 【解析】由题意知,反比例函数图象在第二、四象限,所以3+m<0,即m<-3.故选D. 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源:北师大版数学七年级下册 第1章 整式的乘除 1.2 幂的乘方与积的乘方 幂的乘方 专题练习题 含答案 题型:解答题
若x2n=5,且n为整数,求(x3n)2-5(x2)2n的值.
0 【解析】试题分析:根据幂的乘方进行运算即可. 试题解析:查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 1.5 平方差公式 同步测试 题型:填空题
在一个边长为11.75cm的正方形纸板内,剪去一个边长为8.25cm的正方形,剩下部分的面积等于__cm2.
70 【解析】试题解析:剩下部分的面积是11.752-8.252=(11.75+8.25)(11.75-8.25)=20×3.5=70, 故答案为:70.查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:单选题
如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A.C分别在x轴、y轴上,反比例函数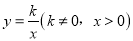 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=450,MN=2,则点C的坐标为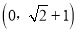 .
.
其中正确的个数是( )
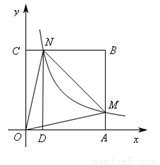
A.1 B.2 C.3 D.4
C. 【解析】 试题分析:设正方形OABC的边长为a, 则A(a,0),B(a,a),C(0,a),M(a,),N(,a). ∵CN=AM=,OC=OA= a,∠OCN=∠OAM=900,∴△OCN≌△OAM(SAS).结论①正确. 根据勾股定理,,,∴ON和MN不一定相等.结论②错误. ∵,∴.结论③正确. 如图,过点O作OH⊥MN于点H,则 ∵△...查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:填空题
已知反比例函数的图象经过点(2,-1 ),则这个反比例函数的表达式为 .
【解析】 试题分析:设反比例函数解析式为,再把(2,-1 )代入,即可求得结果. 设反比例函数解析式为, ∵图象经过点(2,-1 ), ,, 这个反比例函数的表达式为.查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:单选题
下面的函数是反比例函数的是( )
A. y=3x-1 B. y=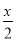 C. y=
C. y=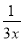 D. y=
D. y=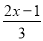
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第1章 有理数 单元测试卷 题型:填空题
填在下面各正方形中的四个数之间都有一定的规律,据此规律得出a+b+c=________.
110 【解析】试题分析:根据前三个正方形中的数字规律可知:C所处的位置上的数字是连续的奇数,所以c=9,而a所处的位置上的数字是连续的偶数,所以a=10,而b=ac+1=9×10+1=91,所以a+b+c=9+10+91=110.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第1章 有理数 单元测试卷 题型:单选题
有理数(-1)2,(-1)3,-12,|-1|,-(-1), 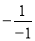 中,化简结果等于1的个数是( )
中,化简结果等于1的个数是( )
A. 3个 B. 4个 C. 5个 D. 6个
B 【解析】∵(-1)2=1,(-1)3=-1,-12=-1,|-1|=1,-(-1)=1, =1, ∴化简结果等于1的个数有4个, 故选B.查看答案和解析>>
科目:初中数学 来源:四川省仁寿县2017-2018学年上学期八年级期末考试数学试卷 题型:单选题
如图,△ABC的外角∠ACD的平分线CP与∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP的度数是( )
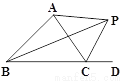
A. 30°; B. 40°; C. 50°; D. 60°.
C 【解析】过点P作PE⊥BD于点E,PF⊥BA于点F,PH⊥AC于点H, ∵CP平分∠ACD,BP平分∠ABC, ∴PE=PH,PE=PF,∠PCD=∠ACD,∠PBC=∠ABC, ∴PH=PF, ∴点P在∠CAF的角平分线上, ∴AP平分∠FAC, ∴∠CAP=∠CAF. ∵∠PCD=∠BPC+∠PBC, ∴∠ACD=2∠BPC+2∠PBC...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com