练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

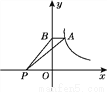
    如图，点A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，且△ABP的面积为6，则这个反比例函数的表达式为________．

    【解析】连接OA，则△ABP与△ABO的面积都等于6，根据反比例函数k的几何意义可得反比例函数的表达式是y＝.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型：单选题

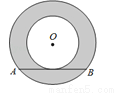
    如图，两圆圆心相同，大圆的弦AB与小圆相切，AB=8，则图中阴影部分的面积是（　　）

    A. 8π B. 4π C. 64π D. 16π

    D 【解析】试题解析：如图， 设AB与小圆切于点C，连结OC，OB. ∵AB与小圆切于点C， ∴OC⊥AB， ∵阴影的面积 又∵直角△OBC中, ∴阴影的面积 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年北师大版七年级数学下1.2幂的乘方与积的乘方同步练习（含答案） 题型：单选题

    若a为有理数,则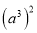的值为( )

    A. 负数 B. 正数 C. 零或负数 D. 正数或零

    D 【解析】试题解析：∵a为有理数, 的值为正数或零. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第一章 整式的乘除 1.5 平方差公式 同步测试 题型：单选题

    下列式中能用平方差公式计算的有( )

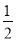    ①(x－y)(x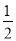＋y)；②(3a－bc)(－bc－3a)；③(100＋1)(100－1)；④(x＋1)(y－1)．

    A. 1个 B. 2个

    C. 3个 D. 4个

    C 【解析】试题解析：：①（x-y）（x+y）=x2-y2； ②（3a-bc）（-bc-3a）=b2c2-9a2； ③（100+1）（100-1）=10000-1=9999； ④(x＋1)(y－1)=xy-x+y-1， 所以能用平方差公式计算的有3个． 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十六章 达标检测卷 题型：解答题

    已知反比例函数y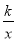＝，当x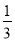＝－时，y＝－6.

    (1)这个函数的图象位于哪些象限？y随x的增大如何变化？

    (2)当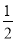＜x＜4时，求y的取值范围．

    (1)见解析；（2）＜y＜4. 【解析】试题分析：（1）把x＝－，y＝－6代入y＝中，求得k值，根据反比例函数的性质即可得结论；（2）将x＝代入表达式中得y＝4，将x＝4代入表达式中得y＝，根据反比例函数的性质即可得结论. 试题解析： (1)把x＝－，y＝－6代入y＝中，得－6＝， 则k＝2，即反比例函数的表达式为y＝. 因为k＞0，所以这个函数的图象位于第一、第三象...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十六章 达标检测卷 题型：单选题

    如图，△AOB是直角三角形，∠AOB＝90°，OB＝2OA，点A在反比例函数y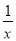＝的图象上．若点B在反比例函数y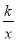＝的图象上，则k的值为( )

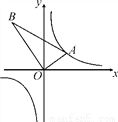
    A. －4 B. 4 C. －2 D. 2

    A 【解析】试题解析：过点A，B作AC⊥x轴，BD⊥x轴，分别于C，D． 设点A的坐标是（m，n），则AC=n，OC=m， ∵∠AOB=90°， ∴∠AOC+∠BOD=90°， ∵∠DBO+∠BOD=90°， ∴∠DBO=∠AOC， ∵∠BDO=∠ACO=90°， ∴△BDO∽△OCA， ∴， ∵OB=2OA， ∴BD=2m，OD=...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十六章 达标检测卷 题型：单选题

    若点A（a，b）在反比例函数的图像上，则代数式ab-4的值为（ ）

    A. 0 B. -2 C. 2 D. -6

    B 【解析】试题解析：∵点（a，b）反比例函数上， ∴b=，即ab=2， ∴原式=2-4=-2． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第1章 有理数 单元测试卷 题型：单选题

    下列算式正确的是(　　)

    A. (－14)－5＝－9 B. 0－(－3)＝3 C. (－3)－(－3)＝－6 D. |5－3|＝－(5－3)

    B 【解析】根据有理数的减法，减去一个数等于加上这个数的相反数，可知：（-14)-(+5)=（-14）+（-5）=-19；0-(-3)=0+（+3）=3；(-3)-(-3)=（-3）+3=0；︱5-3︱=5-3=2. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：四川省仁寿县2017-2018学年上学期八年级期末考试数学试卷 题型：填空题

    在锐角△ABC中，BC=8，∠ABC=30°，BD平分∠ABC，M、N分别是BD、BC上的动点，则CM+MN的最小值是_______.

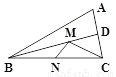
    4. 【解析】如下图，设点N关于BD的对称点为N′，连接MN′，则MN′=MN， ∴CM+MN=CM+MN′， ∵BD平分∠ABC， ∴点N′在BA上， ∴当C、M、N′在同一直线上，且CN′⊥AB时，CM+MN最短， 过点C作CE⊥AB于点E，则CE的长是CM+MN的最小值， ∴∠CEB=90°， 又∵∠ABC=30°， ∴CE=BC=4， ...

    查看答案和解析>>

    同步练习册答案