练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列运算中，正确的是（   ）

    A. （x+y）2=x2+y2  B. x6÷x3=x2 C. ﹣2（x﹣1）=﹣2x+2 D. 2﹣1=﹣2

    C 【解析】（x+y）2=x2+2xy+y2，A选项错误； x6÷x3=x6－3 =x3，B选项错误； －2（x－1）=－2x+2，C选项正确； 2﹣1=，D选项错误. 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年河北省沧州市中考数学模拟试卷（九） 题型：单选题

    由4个相同的小立方体搭成的几何体如图所示，则它的主视图是（　　）

    A. B. C. D.

    A 【解析】试题分析：几何体的主视图有2列，每列小正方形数目分别为2，1. 故选A．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古乌海市七年级（下）期末数学试卷 题型：单选题

    如图，△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的，若△ABC的面积为20cm2，则四边形A1DCC1的面积为（　　）

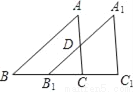
    A. 10 cm2 B. 12 cm2 C. 15 cm2 D. 17 cm2

    C 【解析】【解析】 ∵△A1B1C1是由ABC沿BC方向平移了BC长度的一半得到的， ∴AC∥AC1，B1C=B1C1， ∴△B1DC∽△B1A1C1， ∵△B1DC与△B1A1C1的面积比为1：4， ∴四边形A1DCC1的面积是△ABC的面积的， ∴四边形A1DCC1的面积是：， 故选C。

    查看答案和解析>>

    科目：初中数学 来源：广东省2017年中考数学一模试卷 题型：解答题

    解不等式组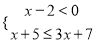，并将解集在数轴上表示．

    不等式组的解集是﹣1≤x＜2，在数轴上表示不等式组的解集见解析. 【解析】试题分析：分别解出两个不等式的解，求出两个解公共的部分，再在数轴上表示出来即可. 试题解析： 【解析】 由①得，x＜2， 由②得，x≥－1， 不等式组的解集是：－1≤x＜2， 在数轴上表示不等式组的解集为：

    查看答案和解析>>

    科目：初中数学 来源：广东省2017年中考数学一模试卷 题型：单选题

    如图，路灯距地面8米，身高1.6米的小明从距离灯底（点O）20米的点A处，沿AO所在直线行走12米到达点B时，小明身影长度（   ）

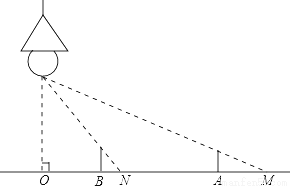
    A. 变长2.5米 B. 变短2米 C. 变短2.5米 D. 变短3米

    D 【解析】 由题意得：OC=8，AB=12，OA=20，BD=1.6， ∴OB=OA－AB=12， ∵∠DBN=∠O=90°，∠CNO=∠DNB， ∴△DBN∽△CON， ∴=, 设BN=x，则ON=8+x， ∴=, 解得x=2. ∴BN=2， 同理可得：AM=5， ∴小明身影长度变短了3m. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学三模试卷 题型：解答题

    如图，平行四边形OBCD中，OB=8cm，BC=6cm，∠DOB=45°，点P从O沿OB边向点B移动，点Q从点B沿BC边向点C移动，P，Q同时出发，速度都是1cm/s．

    （1）求经过O，B，D三点的抛物线的解析式；

    （2）判断P，Q移动几秒时，△PBQ为等腰三角形；

    （3）若允许P点越过B点在BC上运动，Q点越过C点在CD上运动，设线PQ与OB，BC，DC围成的图形面积为y（cm2），点P，Q的移动时间为t（s），请写出y与t之间的函数关系式，并写出t的取值范围．

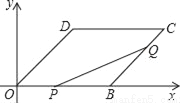
    （1）y=﹣；（2）P，Q移动4秒时，△PBQ为等腰三角形；（3）y与t之间的函数关系式为y=t2﹣5t+45，t的取值范围为8＜t≤14． 【解析】【解析】 （1）过点D作DM⊥OB于M， ∵平行四边形OBCD中，OB=8cm，BC=6cm，∠DOB=45°， ∴OD=BC=6cm， ∴OM=DM=OD•sin45°=6×=3， ∴D（3，3），B（8，0）， ...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学三模试卷 题型：单选题

    下列说法不正确的是（　　）

    A. 一组数据中，平均数、众数、中位数可能都相同

    B. 一组数据平均数一定大于其中每一个数据

    C. 在频率分布直方图中，每个小长方形的面积等于相应小组的频率

    D. 样本的容量越大，对总体的估计越精确

    B 【解析】试题解析： A.一组数据中，平均数、众数、中位数可能都相同，故说法正确； B.一组数据平均数不可能大于其中每一个数据，故说法错误； C.在频率分布直方图中，每个小长方形的面积等于相应小组的频率，说法正确； D.样本的容量越大，对总体的估计越精确，说法正确； 故选B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省徐州市丰县2018届九年级上学期第二次月考数学试卷 题型：解答题

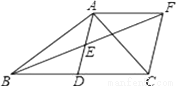
    如图，在△ABC中，∠BAC=90°，AD是中线，E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．

    （1）求证：AD=AF；

    （2）如果AB=AC，试判断四边形ADCF的形状，并证明你的结论．

    （1）详见解析；（2）四边形ADCF是正方形，证明详见解析. 【解析】试题分析：（1）由E是AD的中点，AF∥BC，易证得△AEF≌△DEB，即可得AD=BD，又由在△ABC中，∠BAC=90°，AD是中线，根据直角三角形斜边的中线等于斜边的一半，即可证得AD=BD=CD=BC，即可证得：AD=AF； （2）由AF=BD=DC，AF∥BC，可证得：四边形ADCF是平行四边形，又由AB=...

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年陕西省七年级（下）第二次测验数学试卷 题型：解答题

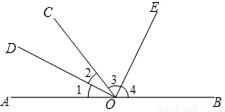
    如图，O为直线AB上的一点，∠AOC=50°，OD平分AOC，∠DOE=90°

    ①求∠BOD的度数；

    ②OE是∠BOC的平分线吗？为什么？

    (1) ∠BOD的度数为：155°;(2)见解析 【解析】试题分析：（1）先根据角平分线的性质，求出∠1和∠2的度数，然后根据互补两角的关系求解； （2）通过角的和差关系求出∠COE和∠BOE的度数，然后得到角平分线OE. 试题解析：①∵∠AOC=50°，OD平分AOC， ∴∠1=∠2=∠AOC=25°， ∴∠BOD的度数为：180°﹣25°=155°； ②∵∠...

    查看答案和解析>>

    同步练习册答案