练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    将一元二次方程x2-4x-6=0化成（x-a）2=b的形式，则b等于（　　）

    A. 4 B. 6 C. 8 D. 10

    D 【解析】利用配方法即可得出答案. 【解析】 ∵， ， ， ， ∴b＝10. 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：上海市普陀区（五四制）2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    下列等式中，从左到右的变形是因式分解的是（ ）

    A. 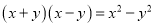B. 42=2×3×7

    C. 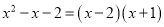D.

    C 【解析】A. ∵是乘法运算，故不正确； B. ∵42=2×3×7是分解因数，故不正确；； C. ∵是因式分解，故正确；； D. ∵的右边不是积的形式，不是因式分解，故不正确；． 故选C.

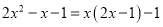
    查看答案和解析>>

    科目：初中数学 来源：北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型：填空题

    如图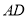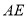， ， 是正六边形的两条对角线.在不添加任何其他线段的情况下，请写出两个关于图中角度的正确结论：（1）__________________________；（2）______________________.

    ∠F=∠E ∠F=120° 【解析】试题解析：【解析】 (1)∠F=∠E；(2)∠F=120°．答案不唯一．故答案为：(1)∠F=∠E；(2)∠F=120°（答案不唯一）．

    查看答案和解析>>

    科目：初中数学 来源：海南省定安县2018届九年级上学期期末考试数学试卷 题型：解答题

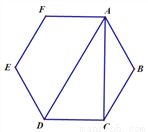
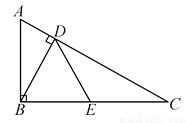
    如图，在Rt△ABC中，∠ABC＝90°，BD⊥AC于点D ，点E为线段BC的中点，AD＝2，tan A＝2．

    （1）求AB的长；

    （2）求DE的长．

    （1）AB＝；（2）DE＝． 【解析】（1）利用∠A的正切值求出BD的长，再利用勾股定理即可求出AB； （2）利用∠A的正切值求出BC的长，再根据直角三角形斜边上的中线等于斜边的一半即可求出DE的长． 【解析】 （1）∵BD⊥AC，且tan A＝2． ∴， ∵AD＝2， ∴BD＝4， ∴AB＝； （2）在Rt△ABC中， ∵∠ABC＝90°，...

    查看答案和解析>>

    科目：初中数学 来源：海南省定安县2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，在Rt△ABC中，∠C=90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E．若BC=6，则DE的长为（　　）

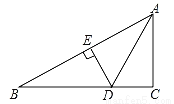
    A. 1 B. 2 C. 3 D. 4

    B 【解析】首先根据角平分线的性质得到DE=DC，∠BAD=∠CAD，由垂直平分线的性质可得AD=BD，结合等边对等角和等量代换的知识可得∠B=∠BAD=∠CAD；然后根据∠C=90°，即可求得∠B=30°，在Rt△BDE中，然后根据含有30°角的直角三角形的性质，得出BD=2DE，即可解答. 【解析】 ∵AD平分∠BAC，∠C=90°，DE⊥AB， ∴DE=DC，∠B+∠BA...

    查看答案和解析>>

    科目：初中数学 来源：海南省定安县2018届九年级上学期期末考试数学试卷 题型：单选题

    顺次连结矩形各边中点所得的四边形是（ ）．

    A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形

    B. 【解析】 试题分析：作出图形，根据三角形的中位线定理可得EF=GH=AC，FG=EH=BD，再根据矩形的对角线相等可得AC=BD，从而得到四边形EFGH的四条边都相等，然后根据四条边都相等的四边形是菱形解答． 如图，连接AC、BD ∵E、F、G、H分别是矩形ABCD的AB、BC、CD、AD边上的中点， ∴EF=GH=AC，FG=EH=BD， ∵矩形ABCD...

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    已知： ， ， ．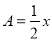

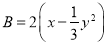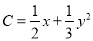    （1）试求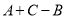所得的结果；（用含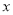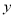， 的式子表示）

    （2）若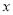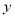， 满足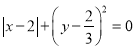，求（1）中所得结果的值．

    （1）-x+y2；（2） 【解析】试题分析：（1）先去括号，再合并即可得到结论； （2）根据非负数的性质得到x，y的值，然后代入计算即可． 试题解析：：（1）A+C－B= +- = +- =-x+y2； （2）因为x，y满足 ∴x+2=0， 解得：x=-2，y=， 代入-x+y2=-（-2）+（）2=2+=.

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    若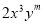与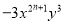是同类项，则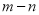的值是（ ）

    A. 3 B. 2 C. 1 D.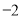

    B 【解析】试题解析：∵单项式与是同类项， ∴2n+1=3，m=3， ∴m=3，n=1， ∴m-n=2， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（人教版）：期中检测题 题型：填空题

    如果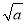的平方根是±3，则＝__________．

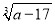    4 【解析】先利用平方根及算术平方根的定义求出a的值，再代入求值即可. 【解析】 ∵的平方根是±3， ∴＝9， ∴ ＝＝＝4. 故答案为：4.

    查看答案和解析>>

    同步练习册答案