
某中学2017届新生入学军训时,小华、小军、小刚的位置如图所示,如果小军的位置用(0,0)表示,小刚的位置用(2,2)表示,那么小华的位置可表示为( )
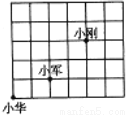
A. (-2,-1) B. (-1,-2) C. (2,1) D. (1,2)
A 【解析】如果小军的位置用(0,0)表示,小刚的位置用(2,2)表示,如图所示就是以小军为原点的平面直角坐标系的第一象限,所以小华的位置为(-2,-1).故选A. 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
如图,在



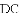





(1)求证:四边形
(2)若
 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源:山东省聊城市莘县2017-2018学年八年级(上)期中数学试卷 题型:单选题
如图,已知点A、D、C、F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
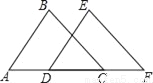
A. BC=EF B. ∠A=∠EDF C. AB∥DE D. ∠BCA=∠F
D 【解析】试题解析:∵AD=CF, ∴AD+CD=CF+DC, ∴AC=DF, A、添加BC=EF可利用SSS定理判定△ABC≌△DEF,故此选项不合题意; B、添加∠A=∠EDF可利用SAS定理判定△ABC≌△DEF,故此选项不合题意; C、添加AB∥DE可证出∠A=∠EDC,可利用SAS定理判定△ABC≌△DEF,故此选项不合题意; D、添加∠BCA...查看答案和解析>>
科目:初中数学 来源:安徽省亳州市利辛县2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
如图所示,△ABC的两条中线AD,BE交于点F,连接CF,若△ABF的面积为8,则△ABC的面积为_____.
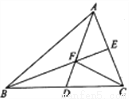
查看答案和解析>>
科目:初中数学 来源:安徽省亳州市利辛县2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列命题中,假命题是( )
A. 三角形的一个外角大于任何一个不相邻的内角
B. 三角形按边可分为不等边三角形、等腰三角形、等边三角形、
C. 三角形中最少有2个锐角
D. 三角形的三条中线交于一点,这个交点就是三角形的重心
B 【解析】选项A、C、D为真命题;选项B, 三角形按边可分为不等边三角形、等腰三角形,等腰三角形又分腰和底边相等的等腰三角形和等边三角形,所以选项B 为假命题,故选B.查看答案和解析>>
科目:初中数学 来源:内蒙古鄂尔多斯市2017-2018学年第一学期期中试卷初一数学. 题型:解答题
整式的加减运算:
(1)化简:-(x2+y2)+[-3xy-(x2-y2)];
(2)先化简,再求值:2(x2y+xy)-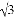 (x2y-
(x2y-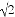 xy)-4xy-x2y)其中x=1,y=-2
xy)-4xy-x2y)其中x=1,y=-2
查看答案和解析>>
科目:初中数学 来源:内蒙古鄂尔多斯市2017-2018学年第一学期期中试卷初一数学. 题型:填空题
若(y-2)2+丨x+1|=0,则xy=__________.
1 【解析】(y-2) ²+丨x+1|=0 ∵(y-2) ²≥0, 丨x+1|≥0, ∴(y-2)=0, x+1=0, ∴y=2,x=-1, ∴xy=(-1) ²=1 故答案为:1.查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区建兰中学2017-2018学年八年级上学期中考试数学试卷 题型:解答题
如图,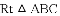
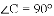
(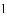
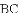
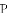
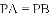
(
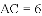
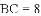
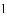

查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷 题型:单选题
如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
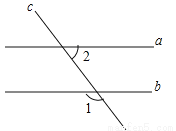
A.50° B.60° C.120° D.130°
B. 【解析】 试题分析:如图,∠3=180°﹣∠1=180°﹣120°=60°,∵a∥b,∴∠2=∠3=60°.故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com